With my thesis available on the arxiv, I thought I should see what I can say about the, as it were, dangling participle of that particular snapshot of this research project. That is, back when I had to declare a title for the thing, quite a long while before I had to finish it, I called it “Extended TQFT’s and Quantum Gravity”, thinking that this would be an accurate title, because it pretty well described the subject of the weekly conversations I’d been having with John while working on it.
However, one thing that gradually becomes clearer as I go further into the process of research is that it’s hard to predict exactly what that process is going to produce. (“Prediction is hard – especially when it comes to the future”, as Yogi Berra said – though possibly it was someone else, since accurate information about the past doesn’t exactly grow on trees either). It turned out that a lot of what I really did was proving some well known folklore theorems about 2-vector spaces; spending a few weeks trying to get a good proof that the weak 2-functor I constructed was actually a weak 2-functor (I still have a kind of unenlightening calculation for a proof); and lots of similarly technical stuff. All of which is – I hope – good mathematics, or at least correct mathematics. But is it physics? All the references to the physical applications were left to the last section, a kind of sketch of where I expect the project to go.
I think the project does indeed have some nice intimate relations to quantum gravity (at least in 3 dimensions), it just didn’t turn out that there was a lot of material about those relations in the document. Instead, there’s a rather impressionistic sketch of how it ought to work. But you might not get the impression that Derek Wise and I started off working on the same project, though we did. Derek’s thesis is not available online in its entirety yet (though part of it appears in this paper on MacDowell-Mansouri gravity and Cartan geometry), but if you check out this this paper by Derek, John, and Alissa Crans, you see a little overlap.
What is the overlap? The physics of it is rooted in a fairly old idea ususally attributed to Wheeler, called “matter without matter” (John cites a number of references on this in week 208 of “This Week’s Finds”). There are several variants of this idea, but all of them in some way contain the key ingredient that matter should somehow be an expression of the shape of spacetime itself. Some older versions hold that elementary particles should be seen as the mouths of little wormholes. More recent ideas, based on spin networks (originally introduced by Roger Penrose in this paper, and much developed since) represent space as a kind of (labelled, directed) graph with edges connecting nodes – and these recent ideas suggest that a stray edge in a spin network will act just like a particle with the spin associated to that edge.
An example of a theory that fits this last picture, and the thing that most directly inspired the project described in my thesis, is some work of Laurent Freidel, David Louapre, and Etera Livine – a series of papers on the Ponzano-Regge model (parts I, II, and III) which is a model of 3-dimensional Riemannian quantum gravity. This is pretty unphysical – since the standard picture of gravity in the physical world is in terms of 4-dimensional, Lorentzian gravity (which, unlike the Riemannian picture, distinguishes between spacelike and timelike directions). Nevertheless, most people would accept the Ponzano-Regge model as physics… Anyway, their model describes a world where gravity is described by the Ponzano-Regge model, and is coupled to matter which is represented as stray ends of edges in the spin network. As the networks evolve, the stray edges trace out Feynman diagrams for the matter in question.
I could also mention that Laurent, together with Aristide Baratin, has recently done some work going in the other direction – starting with Feynman diagrams and trying to show how a picture of quantum gravity was already hidden in them, but with the gravitational coupling “turned off”. They have a couple of papers doing this in both three and four dimensions.
In any case, this version of “matter without matter” was a major part of the inspiration for
this project, but I describe things from a somewhat different point of view – or at least a dual point of view. When you describing the geometry of space in terms of a spin network, nodes in the network represent volumes in space, and edges in the network represent boundaries between volumes. This is a Poicaré dual picture – it’s also a picture that depends on a triangulation, or some other way of breaking a manifold apart into cells. I allude to this in the beginning of the thesis, talking about the Fukuma-Hosono-Kawai construction for getting a topological quantum field theory in 2 dimensions. However, one of the nice things about this construction is that it ends up being independent of which triangulation you pick (I have an explanation of this in these slides for a talk I gave last year at the Perimeter Institute). So after a bit, we just end up thinking of matter as living on boundaries of some kind.
The idea is that you have a manifold supporting some sort of geometric structure. The manifold has some “defects” – boundaries where that structure has to stop. It could be a 2D surface with some holes bunched out with a hole-punch – holes with a 1D boundary. Or it could be a 3D space with some 2D surface as the boundary. These could be literal defects – the boundaries describe where a pointlike, or line-like “flaw” in the geometry can live, because part of the manifold is just missing. This is the usual way of thinking about singularities. Or, you can just imagine that the boundary marks out some kind of “system” sitting in space that you might want to observe, and the theory tells you what information about the system on the other side of that boundary can be detected by looking at the geometric structure of the space around it.
Now, if we’re looking at 3D space, then gravity is fairly simple. Up to equivalence (i.e. up to a change of coordinates) the information about matter which we expect to be carried by the geometry of the space it lives in would include its (rest) mass and its momentum – in particular, its angular momentum, or spin. Different types of particles – as far as their effects on gravity allows us to tell them apart – are classified by their masses and spins. Any other information about them doesn’t directly affect the geometry of space. What’s more, in 2-dimensional space, particles look like single points – and all the curvature of space is concentrated at those points, leaving it flat everywhere else. The spin gives information about a “skew” in the geometry of 3D spacetime around the worldlines of such points.
In fact, this is just what this extended TQFT business allows us to recover about – but only because we have information about three levels: “boundaries” (around a system, in which the matter lives), “space”, and “spacetime”. And this is what has to be organized into some kind of 2-category…
(more to come on that in pt 2)
October 3, 2007 at 8:19 pm
But is it physics?
Wow! This puts you right up there with Alain Connes, for your remarkable lack of disdain for the ability of physicists to do physics. Good one. I will certainly be following your interesting posts.
October 3, 2007 at 9:04 pm
[…] TQFT and Gravity — pt 1 […]
October 3, 2007 at 10:34 pm
Kea:
I would hope that a healthy respect for the ability of physicists to grasp their own field wouldn’t be remarkable! The physicists I’ve met have often impressed me with their ability to understand in five minutes, from physical intuition, some concept that it took me months to handle formally. I wish I could do that.
November 5, 2007 at 4:48 am
Hi, Jeff! Hope things are going well for you.
In a 2d TQFT we have a functor
Z:2Cob->Hilb
An action functor does something similar, but the domain is one step down on the categorical ladder:
S:P(X)->R
Usually, P(X) is the category of (homotopy-equivalence classes of) paths in X. But I don’t see any reason why we couldn’t just take it to be 2Cob. Then we get
S:2Cob->R
S(circle) = *
S(cobordism) = real number
We then turn real actions into phases by the usual functor
exp(iS):2Cob->U(1)
So for a cobordism g we have S(g) is a single complex number while Z(g) is a linear transformation, rather like a matrix of complex numbers.
If we know the system is in the state Z(x), then we compute the evolution of the system with
\sum_y \sum_{g:x->y} Z(g) exp(iS(g))
————————————
\sum_y \sum_{g:x->y} exp(iS(g))
Categorifying everything,
Z:3Cob_2->2Hilb
and
S:3Cob_2->Hilb
S(manifold) = *
S(mfld w/ boundary f) = a Hilbert space
S(mfld w/ corners g) = a linear transformation
Now there are two versions of the evolution.
S(f) is a Hilbert-space-valued action; in class we talked about the discrete integral of infinitely many Hilbert spaces where each gets a measure; I presume you could give an imaginary measure, though I haven’t worked that out.
If so, then exp(iS(f)) is also a Hilbert space “scalar” while Z(f) is rather like a matrix of Hilbert spaces and we get some kind of evolution
\bigoplus_b \bigoplus_{f:a->b} Z(f) \tensor exp(iS(f))
——————————————————
\bigoplus_b \bigoplus_{f:a->b} exp(iS(f))
That should be a categorified probability amplitude on the bottom.
Similarly for g, exp(iS(g)) should be a linear transformation “scalar” and Z(g) a “matrix of linear transformations” with an evolution
\bigoplus_y \bigoplus_{g:x->y} Z(g) \tensor exp(iS(g))
——————————————————
\bigoplus_y \bigoplus_{g:x->y} exp(iS(g))
What should I make of this abstract nonsense? When I square the magnitude of a complex number, I can interpret the result as a probability. How do I interpret a Hilbert space as anything like a probability?
November 5, 2007 at 5:09 pm
Mike: this is a good question. I’m not sure how to interpret the division you do in the normalization, but I would interpret the categorified version of an amplitude, which is a vector (Hilbert) space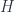 , as an internal space of states for some “2-state”. Then the “categorified probability” is a derived space
, as an internal space of states for some “2-state”. Then the “categorified probability” is a derived space  . The partition function which serves as a normalizing factor would then be a sum over all possible 2-states of the corresponding internal spaces. This could be like a “total space” for a whole system, no longer divided up into different 2-states. A low probability event corresponds to one whose internal state space gives a low-dimensional subspace of this total space.
. The partition function which serves as a normalizing factor would then be a sum over all possible 2-states of the corresponding internal spaces. This could be like a “total space” for a whole system, no longer divided up into different 2-states. A low probability event corresponds to one whose internal state space gives a low-dimensional subspace of this total space.
At least, this is the best interpretation I’ve come up with so far. It’s the one I advocated in the talk I gave in Iowa, for which some slides should be up shortly.