So last time I was describing this “matter without matter” idea and claiming that it has something to do with TQFT and the Ponzano-Regge model of quantum gravity. I’d like to get a little more detailed here.
To describe this in physics terms, it’s easiest to understand the point if, instead of using the (more technically accurate) terms “manifold”, “cobordism between manfolds”, and “cobordism with corners between cobordisms, I name-drop the terms “boundary”, “space”, and “spacetime”. But the caveat here is that these terms really imply a certain geometric structure which I’m not actually assuming is there: a specific geometric structure on these manifolds is a state of the theory. Furthermore, with Ponzano-Regge, we’re talking about Riemannian gravity – there’s no such thing as a “timelike” direction. So using the term “spacetime” is being rather optimistic that everything will work out in more physical settings – but it’s a helpful motivation.
At any rate, the way I describe it in the thesis, in dimensions the typical setup for an extended TQFT in the sense of a weak 2-functor into 2-Vect, one has “boundaries”, which are manifolds of
dimension (in 3D, each boundary is some union of a bunch of circles, and in 4D it would be a union of surfaces, each with some genus). These are joined by “spaces” (cobordisms), of
dimensions, which are in turn connected by “spacetimes” (with the above caveat). These cobordisms are, in particular, cospans in some category of spaces, and they give rise to spans of groupoids of configurations for a gauge theory.
In any case, how does this relate to gravity? The answer is by way of topological gauge theory: the extended TQFT in question has a lot to do with flat connections on manifolds (or indeed manifolds with boundary or corners), which is what topological gauge theory is about. One way to say what a flat connection is, is to say that it takes a path in the space
, and gives an element of the gauge group
(this is not the most well-known way to describe a flat connection – more on that in another post, but I’ll cite weeks 8 and 9 of the spring 2005 UCR Quantum Gravity Seminar for now).
If the gauge group represents the symmetries of something we’re transporting around the surface, this tells us how that thing is being transformed as we move it. For gravity, we take the gauge group to be the symmetries of a model spacetime – what spacetime “looks like locally”. For standard special relativity, this is the Lorentz group
– the symmetries of Minkowski space. For 3D gravity, it’s
(symmetries of Minkowski space with two space and one time dimension). For 3D Riemannian gravity, it’s the group
of rotations in 3D. Actually, I lied: each of these has a double cover, and this is the gauge group (which allows for a spin structure. To simplify a lot of things in my thesis, I talk about the case where
is some finite group, but eventually I’d like it to be
, the double cover of the rotation group
.
So we imagine the connection tells us how an observer would be rotated by the act of moving along a path. (There is a kind of trivialization of a bundle lurking behind this glib statement, but I’m putting that off). Now, some connections are physically the same, even though we describe them differently. They are related by gauge transformations, which are symmetries of the connections themselves. These amount to a way of changing the coordinate system in which we describe (say) our rotation: two rotations of 60 degrees around different axes are not “really” different, since the observer can turn one into the other by tilting her head. What’s traditionally done is to “mod out” by gauge transformations: take any two connections related in this way to be just the same, and throw away any information that distinguishes them. Instead, we can organize flat connections into a category – in fact, a groupoid – where the objects are the connections, and the morphisms are the gauge transformations. We can organize this into the category of functors from the fundamental groupoid of a manifold into the gauge group (thought of as a one-object category).
What’s the point – from a physical point of view – of keeping all the extra structure of these morphisms? To make a long story short, they’re what ends up allowing the theory to classify particles as having spins, not just masses. (Incidentally, I notice that Marni Sheppeard made a guest post on another blog arguing that category theory is useful to physics. Here is another example of how this can be so. Morphisms encode information that would be absent without them, and which has a straightforward physical meaning.)
How does this extra information appear? Well, first of all, what is a point particle, in this model? It’s represented as a boundary around a puncture in “space” – a circular boundary in a 2D surface of some shape or other. The fundamental groupoid of the circle has objects which are points of the circle, and morphisms which are (homotopy classes of) paths. There is an equivalence of categories between this and the fundmental group of the circle, which we can think of as a category with just one object (this is because the circle is a connected space).
Then we’re looking at a category of functors between a couple of one-object categories. Since
, these are determined by the image of the generating path, “1”. So the groupoid of flat connections on this boundary has objects which correpond just to elements of
. But wait! There’s more! You also get natural transformations between these functors! These amount to just conjugations relating elements of
(those “coordinate transformations” I mentioned before). So the whole groupoid has objects corresponding to elements of
, and morphisms
for each
such that
. We call this whole groupoid by the name
– or “
weakly modulo the adjoint action of
.
This is also equivalent (as a category) to a smaller category I’ll call – the “skeleton” of
, namely, a category with one object for each isomorphism class of objects in
(i.e. each conjugacy class in
). Each of these has a group (the original category was a groupoid, so the new one is also) of automorphisms. This will be the same as the group of automorphisms of the corresponding object in
– namely, the stabilizer subgroup of that element of
, which, if
is generically
, except for a couple of exceptional points corresponding to 0-degree and 360-degree rotations.
Finally, a 2-vector in the 2-vector space assigned to the circle (which I like to think of as a “2-state”) is a functor from this into
. Each such functor
is a direct sum of a bunch of irreducible ones, and the irreducible ones assign a nontrivial vector space
to just one object
– and the group of automorphisms of that object are taken to a group of automorphisms of
. That is,
is specified by a conjugacy class of
, and a representation of its stablizer subgroup. If
, this is an angle and a spin. And in 3D gravity, the mass of a particle corresponds to an angle, because Einstein’s equation here says that space is locally flat, except where there is matter – where there is an amount of curvature proportional to the mass. This shows up as an “angle deficit” – an amount by which you end up rotated if you travel around the particle.
So that’s how you can see a “hole” in “space” as a point particle with mass and spin in this kind of extended TQFT. In higher dimensions, something similar happens, but the classification is more complicated, because in general the matter looks like “stringy” loops (this is something Derek Wise has looked at in his thesis). Also, above 3D, a theory of flat connections is no longer a theory of gravity, but rather something called BF theory – although in 4D it happens to be a limit of the theory of gravity as you allow Newton’s constant to approach zero. (That is, it describes the topological sector of the theory of gravity.)
What I haven’t yet explained is how this matter, which so far has the properties we might hope for, also gets to live in a spacetime governed by the Ponzano-Regge model. That means looking at what the extended TQFT does to the morphisms and 2-morphisms of the cobordism category – to “space” and to “spacetime”, and what the “2-linear maps” and “transformations” they give are like. Tune in next installment…
October 4, 2007 at 9:41 pm
What does this look like if ? Suffice to say that I’ve looked at a very similar picture myself for (seemingly) very different reasons, and that gauge group has been important for me.
? Suffice to say that I’ve looked at a very similar picture myself for (seemingly) very different reasons, and that gauge group has been important for me.
October 4, 2007 at 11:11 pm
There’s a really good answer to that question in Derek’s thesis, where he talks about “particle types in Chern-Simons gravity” among a good many other things. Infortunately I can’t point you to it yet. However, here’s a quick summary…
If , we have a similar scenario to the one I described, except that instead of the double cover of the rotation group
, we have a similar scenario to the one I described, except that instead of the double cover of the rotation group  , it is the double cover of the Lorentz group
, it is the double cover of the Lorentz group  . Which is great, BTW, if you want something physical – this is the symmetry group for flat Minkowski spacetime… Being noncompact makes it a bit harder to deal with for my purposes, but this “particle type” part of the analysis works just fine. Once again, flat connections aren’t exactly “real” gravity. And if you want to put this in a 4D spacetime, things again get a little more complicated, involving strings, and something a bit fancier than just equivalence classes, etc.
. Which is great, BTW, if you want something physical – this is the symmetry group for flat Minkowski spacetime… Being noncompact makes it a bit harder to deal with for my purposes, but this “particle type” part of the analysis works just fine. Once again, flat connections aren’t exactly “real” gravity. And if you want to put this in a 4D spacetime, things again get a little more complicated, involving strings, and something a bit fancier than just equivalence classes, etc.
So to recap: for you get “angles” and “spins” from equivalence classes of rotations and representations of stabilizer subgroups. So the thing is to classify equivalence classes and stabilizers in
you get “angles” and “spins” from equivalence classes of rotations and representations of stabilizer subgroups. So the thing is to classify equivalence classes and stabilizers in  .
.
For , the equivalence classes come in a few different flavours. There are some oddballs like the identity, but the general case I think fall into three classes: elements corresponding to (a) rotations, (b) boosts, and (c) loxodromic transformations. These correspond to diagonal matrices with complex conjugate eigenvalues, one of which is
, the equivalence classes come in a few different flavours. There are some oddballs like the identity, but the general case I think fall into three classes: elements corresponding to (a) rotations, (b) boosts, and (c) loxodromic transformations. These correspond to diagonal matrices with complex conjugate eigenvalues, one of which is  , where
, where 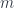 gets to be called the “mass” of the particle. The three cases are where
gets to be called the “mass” of the particle. The three cases are where 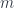 is (a) real (and bounded), (b) purely imaginary (and unbounded), (c) complex (with bounded real part). The names for the first two “particle types” (a) tardyons and (b) tachyons (with various masses). I don’t know if there’s a standard name for type (c) – at one point we were despairingly calling them “loxodromons”. They strike me as even more unphysical than the tachyons.
is (a) real (and bounded), (b) purely imaginary (and unbounded), (c) complex (with bounded real part). The names for the first two “particle types” (a) tardyons and (b) tachyons (with various masses). I don’t know if there’s a standard name for type (c) – at one point we were despairingly calling them “loxodromons”. They strike me as even more unphysical than the tachyons.
October 4, 2007 at 11:14 pm
Oh, and BTW, John – can you describe the setting you were looking at? It may be “apparently” very different, but one assumes there must be some underlying reason for being similar. That would be interesting to know about.
October 4, 2007 at 11:29 pm
I’ll track down your email. There are sill some things one must play close to one’s chest.
October 5, 2007 at 3:04 pm
[…] TQFT and Gravity — pt 2 […]
October 6, 2007 at 12:39 pm
Hi Jeffrey,
I am enjoying your paper. Haven’t had too much time to study it, yet, but did note down a couple of remarks here at the $n$-Cafe that occurred to me while looking at the introduction. Am hoping to turn this eventually into a reviewing blog entry as time permits.
It’s certainly great to see this text being finished. I was looking forward to seeing it for quite a while now.
October 6, 2007 at 6:11 pm
Thanks, Urs! I’m working on breaking that big thesis apart into smaller papers, and improving things a bit. Incidentally, I started looking at the paper of yours and Konrad Waldorf’s “Parallel Transport and Functors” partly to that end recently. I hadn’t had a chance to look at it before I was done with the thesis… It’s rather nice – a lot of things that I had some idea of from your blog posts, but gathered together and explained from the beginning.
March 9, 2008 at 6:37 am
[…] the 2-vector space of states it gets in the extended TQFT picture I partially described back here and here. So this is a categorified version of a cohomology module – the non-categorified version […]