I’ve been looking over the last little bit at quantum groupoids, and how they can be used to deform the 2-linearization 2-functor (or into
) which I’ve discussed in here.
First a little motivation: that functor was part of the way I constructed extended TQFT’s. The inclusion realized cobordisms (with corners) in terms of spans of manifolds. Looking at fundamental groupoids using the 2-functor
allows us to think about these in terms of the bicategory
, and then applying
gave 2-Hilbert spaces and 2-linear maps for manifolds and cobordisms (and then natural transformations for cobordisms with corners). Since I made the claim that, with gauge group
– and a suitably infinitary version of
, the extended TQFT gives a theory equivalent to the Ponzano-Regge model of quantum gravity, a reasonable question is: what about the Turaev-Viro model? The PR model is based on labelling edges of a triangulation with representations of
, and the TV model, with representations of
.
Now, the groupoids that show up in the above – groupoids of -connections on a manifold, modulo gauge transformations – are quite closely related to this. In particular, the groupoid of connections for a circle (the basic 1-dimensional manifold that the 3-dimensional theory builds from) is
, the transformation groupoid produced from the action of
on itself by conjugation. (That is: the objects are elements of
, and the morphisms are all the conjugacy relations.) Applying
gives the representation category of this, namely
, so in particular, at the identity of
, one has
as a sub-2-vector space. (The “states” in the 2-Hilbert space for the circle in the ETQFT are labelled by “masses and spins” – the mass=0 case is what gives the representations of
, and for nonzero mass, one has
.)
More broadly: one can describe the state space of a gauge theory – or many other kinds of theory, in terms of transformation groupoids given by symmetries (gauge transformations, say) acting on states (connections, in that case). Is there a way of doing the same for systems whose symmetries are described by quantum groups? If so, then instead of getting 2-vector spaces which are representation categories of groupoids, we should get some which are representation categories of quantum groupoids.
This paper by Ping Xu describes quantum groupoids – or rather, quantum universal enveloping algebras. They’re described here as a “unification of quantum groups and star products” (star products being the partially-defined composition found in groupoids). This paper by Nikshych and Vainerman describes finite quantum groupoids and some applications – in particular, quantum transformation groupoids, which is the immediately relevant application.
First off, quantum groups: these are Hopf algebras, which in particular are bialgebras – they have both a product
and “coproduct”
.
This is because the point here is that we’re following the pattern in which spaces are replaced by algebras: in some simple examples, these are the algebras of functions on a space. The point of noncommutative geometry is that there’s a (contravariant) equivalence between the category of locally compact Hausdorff spaces and the category of commutative algebras, so generalizing to noncommutative algebras (and taking the opposite category) gives a generalization of “locally compact Hausdorff space”. Topological groups like Lie groups are group objects in this category of spaces – and quantum groups are group objects in . So in particular, the group operation shows up as the coproduct
, and the inverse operation is the antipode
.
Of course there are also the unit
and co-unit
(where is the base field, say
). The co-unit is of course the “unit” map for the group object. These maps all satisfy some obvious relations.
Now what about quantum groupoids? These are “groupoid objects” – or rather, models of the theory of groupoids – in . We can’t quite say “groupoid objects”, since a groupoid internal to a category
consists of two objects in
. For example, a Lie groupoid is a groupoid in
, the category of manifolds. It has a base manifold
and a total manifold
, and two maps
, and so forth. The interpretation is that there is a set (or manifold, or what-have-you) of objects, and a set (etc.) of morphisms. There is a (partially-defined) composition operation allowing morphisms to be composed if the source of one is the target of the other, and so forth.
So (a slightly tweaked version of) the definition of a quantum groupoid given by Xu has it consisting of . These unpack in pretty natural ways: it helps to compare to both the definition of, say, a Lie groupoid, and a quantum group.
is the “total algebra$ and
the “base algebra”, and they correspond to the “noncommutative spaces” of morphisms and objects of a groupoid, respectively. Just as a group can be seen as a groupoid with just one object, a quantum group would be a quantum groupoid where the base algebra
is just the base field
.
But then, if is not
, we need some nontrivial
– the source and target maps respectively, which replace the unit map to
. Notice they go from the base
to the total algebra
, not the other way around, because everything works as usual in
. The other maps are likewise dual to those in the definition of a groupoid. The major difference is that we need the equivalent of a partially defined multiplication/composition
and the dual “co-multiplication”/”co-composition”
. This works because using
and
, we get left and right actions of the base
on
, which is thus an
-bimodule, hence we can form the bimodule product
, and thus:
and
The obvious analog of the unit we had for quantum groups is hidden in Xu’s definition (it seems like it should take the place of the requirement that
be unital), but the co-unit
is the dual way of describing the “identity” function .
The antipode plays the role of the inverse map for morphisms
in groupoids.
All these maps have to satisfy various identities which are implied by saying this is a model of the theory of groupoids – check out either of the above papers to see them all explicitly.
(A final observation about the definition: a groupoid is a category which has an inverse map from morphisms to morphisms. If we relax the assumption that we have an antipode , we end up with just the definition of a bialgebroid (having
makes it a “Hopf” algebroid). So “bialgebroid” would seem to be the natural “quantum” version of the concept of a general category…)
So how might one construct such a “quantum action groupoid”? This is addressed (at least in the finite case) in the paper by Nikshych and Vainerman, in their section 2.6. This is generalizing the action groupoid arising from a group acting on a set. The set is replaced by an algebra
(which must be separable, for them – the equivalent of a finite set – and thought of as a “quantum space”). The group
is replaced by a quantum group (or, generally, Hopf algebra)
. The equivalent of having action of the group on the set is that
is a (right)
-module.
Now, the action groupoid for a action on
has for objects the elements of
, and for morphisms, all relations
, which we can write as morphisms
, with source
and target
. The action quantum groupoid associated to the
-module
is the double crossed product
, with multiplication, co-multiplication, etc. defined in fairly natural ways. (Note: those triangles should be semidirect products, but I can’t seem to make that symbol appear here.)
So finally, I seem to be claiming that a such a quantum groupoid, let’s call it is the right “classical” state space (if that’s not too blatant a contradiction in terminology) for a theory having quantum-group symmetry – at least in the categorified picture. No doubt in many cases there is additional structure, capturing the equivalent of, say, symplectic structure, that should also be included (such things certainly can be found in NCG, but I’m still absorbing how exactly).
Then the 2-vector space for the quantized version of such a theory is the category , and a “2-state” just an object in here – a representation of
.
One thing that’s not quite clear to me just now is how this relates to the usual idea of “state” in NCG – a state for a “quantum space” (which is an algebra) being a linear functional on that algebra. Not necessarily a character (i.e. a homomorphism into ), mind you – that would be a 1-dimensional representation, but just a functional.
April 5, 2009 at 4:49 pm
I don’t know much about quantum groupoids. At one point there were a number of competing definitions. One thing I know is that Ross Street has given a definition of quantum category that’s supposed to include quantum groupoids as a special case. Unfortunately I haven’t managed to understand his definition yet.
April 10, 2009 at 12:00 am
John: Thanks for the reference to that paper of Day and Street. It looks like their definition is compatible with the one above, though they’re a little weaker, working in terms of modules, rather than algebras.
A terminological glitch: the other use of the term “quantum category” that I’ve seen was in Frolich and Kerler’s “Quantum Categories, Quantum Groups and Quantum Field Theory”. I don’t have the reference to hand at the moment, but they define a quantum category as some specific kind of braided monoidal category. You reviewed that book in Week 65 and the way you summarized it is that this type of “Quantum Category” is one with properties resembling those of a category of representations of a quantum group at a root of unity.
This overlap of terminology is awkward from my point of view, because of that 2-functor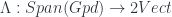 . In particular, any 2-vector space is a special example of a quantum category in Kerler’s sense; on the other hand, a groupoid can be construed as a special case of a quantum category in the sense of Day and Street. In particular, I imagine there would be a generalization of
. In particular, any 2-vector space is a special example of a quantum category in Kerler’s sense; on the other hand, a groupoid can be construed as a special case of a quantum category in the sense of Day and Street. In particular, I imagine there would be a generalization of 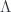 which – at the object level – would take any quantum groupoid (as above) and give its category of representations, which would be a quantum category in the sense of Frolich and Kerler. (And at the morphism level would take cospans to the appropriate kind of functor, etc.) I guess this isn’t so different from how people conflate quantum groups with their categories of representations.
which – at the object level – would take any quantum groupoid (as above) and give its category of representations, which would be a quantum category in the sense of Frolich and Kerler. (And at the morphism level would take cospans to the appropriate kind of functor, etc.) I guess this isn’t so different from how people conflate quantum groups with their categories of representations.