In the first week of November, I was in Montreal for the biannual meeting of the Philosophy of Science Association, at the invitation of Hans Halvorson and Steve Awodey. This was for a special session called “Category Theoretical Reflections on the Foundations of Physics”, which also had talks by Bob Coecke (from Oxford), Klaas Landsman (from Radboud University in Nijmegen), and Gonzalo Reyes (from the University of Montreal). Slides from the talks in this session have been collected here by Steve Awodey. The meeting was pretty big, and there were a lot of talks on a lot of different topics, some more technical, and some less. There were enough sessions relating to physics that I had a full schedule just attending those, although for example there were sessions on biology and cognition which I might otherwise have been interested in sitting in on, with titles like “Biology: Evolution, Genomes and Biochemistry”, “Exploring the Complementarity between Economics and Recent Evolutionary Theory”, “Cognitive Sciences and Neuroscience”, and “Methodological Issues in Cognitive Neuroscience”. And, of course, more fundamental philosophy of science topics like “Fictions and Scientific Realism” and “Kinds: Chemical, Biological and Social”, as well as socially-oriented ones such as “Philosophy of Commercialized Science” and “Improving Peer Review in the Sciences”. However, interesting as these are, one can’t do everything.
In some ways, this was a really great confluence of interests for me – physics and category theory, as seen through a philosophical lens. I don’t know exactly how this session came about, but Hans Halvorson is a philosopher of science who started out in physics (and has now, for example, learned enough category theory to teach the course in it offered at Princeton), and Steve Awodey is a philosopher of mathematics who is interested in category theory in its own right. They managed to get this session brought in to present some of the various ideas about the overlap between category theory and physics to an audience mostly consisting of philosophers, which seems like a good idea. It was also interesting for me to get a view into how philosophers approach these subjects – what kind of questions they ask, how they argue, and so on. As with any well-developed subject, there’s a certain amount of jargon and received ideas that people can refer to – for example, I learned the word and current usage (though not the basic concept) of supervenience, which came up, oh, maybe 5-10 times each day.
There are now a reasonable number of people bringing categorical tools to bear on physics – especially quantum physics. What people who think about the philosophy of science can bring to this research is the usual: careful, clear thinking about the fundamental concepts involved in a way that tries not to get distracted by the technicalities and keep the focus on what is important to the question at hand in a deep way. In this case, the question at hand is physics. Philosophy doesn’t always accomplish this, of course, and sometimes get sidetracked by what some might call “pseudoquestions” – the kind of questions that tend to arise when you use some folk-theory or simple intuitive understanding of some subtler concept that is much better expressed in mathematics. This is why anyone who’s really interested in the philosophy of science needs to learn a lot about science in its own terms. On the whole, this is what they actually do.
And, of course, both mathematicians and physicists try to do this kind of thinking themselves, but in those fields it’s easy – and important! – to spend a lot of time thinking about some technical question, or doing extensive computations, or working out the fiddly details of a proof, and so forth. This is the real substance of the work in those fields – but sometimes the bigger “why” questions, that address what it means or how to interpret the results, get glossed over, or answered on the basis of some superficial analogy. Mind you – one often can’t really assess how a line of research is working out until you’ve been doing the technical stuff for a while. Then the problem is that people who do such thinking professionally – philosophers – are at a loss to understand the material because it’s recent and technical. This is maybe why technical proficiency in science has tended to run ahead of real understanding – people still debate what quantum mechanics “means”, even though we can use it competently enough to build computers, nuclear reactors, interferometers, and so forth.
Anyway – as for the substance of the talks… In our session, since every speaker was a mathematician in some form, they tended to be more technical. You can check out the slides linked to above for more details, but basically, four views of how to draw on category theory to talk about physics were represented. I’ve actually discussed each of them in previous posts, but in summary:
- Bob Coecke, on “Quantum Picturalism”, was addressing the monoidal dagger-category point of view, which looks at describing quantum mechanical operations (generally understood to be happening in a category of Hilbert spaces) purely in terms of the structure of that category, which one can see as a language for handling a particular kind of logic. Monoidal categories, as Peter Selinger as painstakingly documented, can be described using various graphical calculi (essentially, certain categories whose morphisms are variously-decorated “strands”, considered invariant under various kinds of topological moves, are the free monoidal categories with various structures – so anything you can prove using these diagrams is automatically true for any example of such categories). Selinger has also shown that, for the physically interesting case of dagger-compact closed monoidal categories, a theorem is true in general if and only if it’s true for (finite dimensional) Hilbert spaces, which may account for why Hilbert spaces play such a big role in quantum mechanics. This program is based on describing as much of quantum mechanics as possible in terms of this kind of diagrammatic language. This stuff has, in some ways, been explored more through the lens of computer science than physics per se – certainly Selinger is coming from that background. There’s also more on this connection in the “Rosetta Stone” paper by John Baez and Mike Stay,
- My talk (actually third, but I put it here for logical flow) fits this framework, more or less. I was in some sense there representing a viewpoint whose current form is due to Baez and Dolan, namely “groupoidification”. The point is to treat the category
as a “categorification” of (finite dimensional) Hilbert spaces in the sense that there is a representation map
so that phenomena living in
can be explained as the image of phenomena in
. Having done that, there is also a representation of
into 2-Hilbert spaces, which shows up more detail (much more, at the object level, since Tannaka-Krein reconstruction means that the monoidal 2-Hilbert space of representations of a groupoid is, at least in nice cases, enough to completely reconstruct it). This gives structures in
which “conceptually” categorify the structures in
, and are also directly connected to specific Hilbert spaces and maps, even though taking equivalence classes in
definitely doesn’t produce these. A “state” in a 2-Hilbert space is an irreducible representation, though – so there’s a conceptual difference between what “state” means in categorified and standard settings. (There’s a bit more discussion in my notes for the talk than in the slides above.)
- Klaas Landsman was talking about what he calls “Bohrification“, which, on the technical side, makes use of Topos theory. The philosophical point comes from Niels Bohr’s “doctrine of classical concepts” – that one should understand quantum systems using concepts from the classical world. In practice, this means taking a (noncommutative) von Neumann algebra
which describes the observables a quantum system and looking at it via its commutative subalgebras. These are organized into a lattice – in fact, a site. The idea is that the spectrum of
lives in the topos associated to this site: it’s a presheaf that, over each commutative subalgebra
, just gives the spectrum of
. This is philosophically nice in that the “Bohrified” propositions actually behave in a logically sensible way. The topos approach comes from Chris Isham, developed further with Andreas Doring. (Note the series of four papers by both from 2007. Their approach is in some sense dual to that of Lansman, Heunen and Spitters, in the sense that they look at the same site, but look at dual toposes – one of sheaves, the other of cosheaves. The key bit of jargon in Isham and Doring’s approach is “daseinization”, which is a reference to Heidegger’s “Being and Time”. For some reason this makes me imagine Bohr and Heidegger in a room, one standing on the ceiling, one on the floor, disputing which is which.)
- Gonzalo Reyes talked about synthetic differential geometry (SDG) as a setting for building general relativity. SDG is a way of doing differential geometry in a category where infinitesimals are actually available, that is, there is a nontrivial set
. This simplifies discussions of vector fields (tangent vectors will just be infinitesimal vectors in spacetime). A vector field is really a first order DE (and an integral curve tangent to it is a solution), so it’s useful to have, in SDG, the fact that any differentiable curve is, literally, infinitesimally a line. Then the point is that while the gravitational “field” is a second-order DE, so not a field in this sense, the arguments for GR can be reproduced nicely in SDG by talking about infinitesimally-close families of curves following geodesics. Gonzalo’s slides are brief by necessity, but happily, more details of this are in his paper on the subject.
The other sessions I went to were mostly given by philosophers, rather than physicists or mathematicians, though with exceptions. I’ll briefly present my own biased and personal highlights of what I attended. They included sessions titled:
“Quantum Physics“: Edward Slowik talked about the “prehistory of quantum gravity”, basically revisiting the debate between Newton and Leibniz on absolute versus relational space, suggesting that Leibniz’ view of space as a classification of the relation of his “monads” is more in line with relational theories such as spin foams etc. M. Silberstein and W. Stuckey – gave a talk about their “relational blockworld” (described here) which talks about QFT as an approximation to a certain discrete theory, built on a graph, where the nodes of the graph are spacetime events, and using an action functional on the graph.
Meinard Kuhlmann gave an interesting talk about “trope bundles” and AQFT. Trope ontology is an approach to “entities” that doesn’t assume there’s a split between “substrates” (which have no properties themselves), and “properties” which they carry around. (A view of ontology that goes back at least to Aristotle’s “substance” and “accident” distinction, and maybe further for all I know). Instead, this is a “one-category” ontology – the basic things in this ontology are “tropes”, which he defined as “individual property instances” (i.e. as opposed to abstract properties that happen to have instances). “Things” then, are just collections of tropes. To talk about the “identity” of a thing means to pick out certain of the tropes as the core ones that define that thing, and others as peripheral. This struck me initially as a sort of misleading distinction we impose (say, “a sphere” has a core trope of its radial symmetry, and incidental tropes like its colour – but surely the way of picking the object out of the world is human-imposed), until he gave the example from AQFT. To make a long story short, in this setup, the key entites are something like elementary particles, and the core tropes are those properties that define an irreducible representation of a -algebra (things like mass, spin, charge, etc.), whereas the non-core tropes are those that identify a state vector within such a representation: the attributes of the particle that change over time.
I’m not totally convinced by the “trope” part of this (surely there are lots of choices of the properties which determine a representation, but I don’t see the need to give those properties the burden of being the only ontologically primaries), but I also happen to like the conclusions because in the 2Hilbert picture, irreducible representations are states in a 2-Hilbert space, which are best thought of as morphisms, and the state vectors in their components are best thought of in terms of 2-morphisms. An interpretation of that setup says that the 1-morphism states define which system one’s talking about, and the 2-morphism states describe what it’s doing.
“New Directions Concerning Quantum Indistinguishability“: I only caught a couple of the talks in this session, notably missing Nick Huggett’s “Expanding the Horizons of Quantum Statistical Mechanics”. There were talks by John Earman (“The Concept of Indistinguishable Particles in Quantum
Mechanics”), and by Adam Caulton (based on work with Jeremy Butterfield) on “On the Physical Content of the Indistinguishability Postulate”. These are all about the idea of indistinguishable particles, and the statistics thereof. Conventionally, in QM you only talk about bosons and fermions – one way to say what this means is that the permutation group naturally acts on a system of
particles, and it acts either trivially (not altering the state vector at all), or by sign (each swap of two particles multiplies the state vector by a minus sign). This amounts to saying that only one-dimensional representations of
occur. It is usually justified by the “spin-statistics theorem“, relating it to the fact that particles have either integer or half-integer spins (classifying representations of the rotation group). But there are other representations of
, labelled by Young diagrams, though they are more than one-dimensional. This gives rise to “paraparticle” statistics. On the other hand, permuting particles in two dimensions is not homotopically trivial, so one ought to use the braid group
, rather than
, and this gives rise again to different statistics, called “anyonic” statistics.
One recurring idea is that, to deal with paraparticle statistics, one needs to change the formalism of QM a bit, and expand the idea of a “state vector” (or rather, ray) to a “generalized ray” which has more dimensions – corresponding to the dimension of the representation of one wants the particles to have. Anyons can be dealt with a little more conventionally, since a 2D system may already have them. Adam Caulton’s talk described how this can be seen as a topological phenomenon or a dynamical one – making an analogy with the Bohm-Aharonov effect, where the holonomy of an EM field around a solenoid can be described either dynamically with an interacting Lagrangian on flat space, or topologically with a free Lagrangian in space where the solenoid has been removed.
“Quantum Mechanics“: A talk by Elias Okon and Craig Callender about QM and the Equivalence Principle, based on this. There has been some discussion recently as to whether quantum mechanics is compatible with the principle that relates gravitational and inertial mass. They point out that there are several versions of this principle, and that although QM is incompatible with some versions, these aren’t the versions that actually produce general relativity. (For example, objects with large and small masses fall differently in quantum physics, because though the mean travel time is the same, the variance is different. But this is not a problem for GR, which only demands that all matter responds dynamically to the same metric.) Also, talks by Peter Lewis on problems with the so-called “transactional interpretation” of QM, and Bryan Roberts on time-reversal.
“Why I Care About What I Don’t Yet Know“: A funny name for a session about time-asymmetry, which is the essentially philosophical problem of why, if the laws of physics are time-symmetric (which they approximately are for most purposes), what we actually experience isn’t. Personally, the best philosophical account of this I’ve read is Huw Price’s “Time’s Arrow“, though Reichenbach’s “The Direction of Time” has good stuff in it also, and there’s also Zeh’s more technical “The Physical Basis of the Direction of Time“. In the session, Chris Suhler and Craig Callender gave an account of how, given causal asymmetry, our subjective asymmetry of values for the future and the past can arise (the intuitively obvious point being that if we can influence the future and not the past, we tend to value it more). Mathias Frisch talked about radiation asymmetry (the fact that it’s equally possible in EM to have waves converging on a source than spreading out from it, yet we don’t see this). Owen Maroney argued that “There’s No Route from Thermodynamics to the Information Asymmetry” by describing in principle how to construct a time-reversed (probabilisitic) computer. David Wallace spoke on “The Logic of the Past Hypothesis”, the idea inspired by Boltzmann that we see time-asymmetry because there is a point in what we call the “past” where entropy was very low, and so we perceive the direction away from that state as “forward” it time because the world tends to move toward equilibrium (though he pointed out that for dynamical reasons, the world can easily stay far away from equilibrium for a long time). He went on to discuss the logic of this argument, and the idea of a “simple” (i.e. easy-to-describe) distribution, and the conjecture that the evolution of these will generally be describable in terms of an evolution that uses “coarse graining” (i.e. that repeatedly throws away microscopic information).
“The Emergence of Spacetime in Quantum Theories of Gravity“: This session addressed the idea that spacetime (or in some cases, just space) might not be fundamental, but could emerge from a more basic theory. Christian Wüthrich spoke about “A-Priori versus A-Posteriori” versions of this idea, mostly focusing on ideas such as LQG and causal sets, which start with discrete structures, and get manifolds as approximations to them. Nick Huggett gave an overview of noncommutative geometry for the philosophically minded audience, explaining how an algebra of observables can be treated like space by means of all the concepts from geometry which can be imported into the theory of -algebras, where space would be an approximate description of the algebra by letting the noncommutativity drop out of sight in some limit (which would be described as a “large scale” limit). Sean Carroll discussed the possibility that “Space is Not Fundamental – But Time Might Be”, pointing out that even in classical mechanics, space is not a fundamental notion (since it’s possible to reformulate even Hamiltonian classical mechanics without making essential distinctions between position and momentum coordinates), and suggesting that space arises from the dynamics of an actual physical system – a Hamiltonian, in this example – by the principle “Position Is The Thing In Which Interactions Are Local”. Finally, Sean Maudlin gave an argument for the fundamentality of time by showing how to reconstruct topology in space from a “linear structure” on points saying what a (directed!) path among the points is.
July 13, 2011 at 7:54 am
Hi, Jeff. What is known about Tannakian reconstruction and the groupoidification program? If one goal is to replace the representation theory of a group in vector spaces by spans of groupoids over
in vector spaces by spans of groupoids over  , I take it one can recover
, I take it one can recover  from the later.
from the later.
July 20, 2011 at 11:00 am
Hi David.
I haven’t thought as much as, say, Alex Hoffnung about groupoidification of representation theory itself. But certainly if, after applying the degroupoidification functor , one gets the usual vector spaces carrying representations of
, one gets the usual vector spaces carrying representations of  , then that should be enough to use the usual Tannakian reconstruction theorem. We’d have a category of objects, and a functor giving underlying vector spaces.
, then that should be enough to use the usual Tannakian reconstruction theorem. We’d have a category of objects, and a functor giving underlying vector spaces.
To do this directly, the category in question might not be that of groupoids over , but only its image in
, but only its image in  after applying
after applying 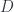 (the only obstacle I see would be that degroupoidification might not be the right kind of forgetful functor for the usual Tannakian reconstruction to work).
(the only obstacle I see would be that degroupoidification might not be the right kind of forgetful functor for the usual Tannakian reconstruction to work).
A different connection to Tannakian reconstruction is via this “2-linearization”, in which we look at the image of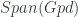 in
in  rather than
rather than  . The 2-vector space associated to a groupoid would be its representation category. Thinking of this as a functor category into vector spaces, this construction naturally gives this AS a concrete category. So the data that comes out of 2-linearization should be enough to reconstruct the groupoids on either end of the span. In general one doesn’t get enough to reconstruct the span from the 2-linear map associated to it, though (for the same reason you can’t reconstruct a groupoid from its degroupoidification, which is a vector space).
. The 2-vector space associated to a groupoid would be its representation category. Thinking of this as a functor category into vector spaces, this construction naturally gives this AS a concrete category. So the data that comes out of 2-linearization should be enough to reconstruct the groupoids on either end of the span. In general one doesn’t get enough to reconstruct the span from the 2-linear map associated to it, though (for the same reason you can’t reconstruct a groupoid from its degroupoidification, which is a vector space).
July 20, 2011 at 3:56 pm
Thanks for this. I’ll link from the Cafe to see if there’s a discussion to be had.