Higher Gauge Theory in Edinburgh – Part III

Why Higher Geometric Quantization

The largest single presentation was a pair of talks on “The Motivation for Higher Geometric Quantum Field Theory” by Urs Schreiber, running to about two and a half hours, based on these notes. This was probably the clearest introduction I’ve seen so far to the motivation for the program he’s been developing for several years. Broadly, the idea is to develop a higher-categorical analog of geometric quantization (GQ for short).

One guiding idea behind this is that we should really be interested in quantization over (higher) stacks, rather than merely spaces. This leads inexorably to a higher-categorical version of GQ itself. The starting point, though, is that the defining features of stacks capture two crucial principles from physics: the gauge principle, and locality. The gauge principle means that we need to keep track not just of connections, but gauge transformations, which form respectively the objects and morphisms of a groupoid. “Locality” means that these groupoids of configurations of a physical field on spacetime is determined by its local configuration on regions as small as you like (together with information about how to glue together the data on small regions into larger regions).

Some particularly simple cases can be described globally: a scalar field gives the space of all scalar functions, namely maps into ; sigma models generalise this to the space of maps for some other target space. These are determined by their values pointwise, so of course are local.

More generally, physicists think of a field theory as given by a fibre bundle (the previous examples being described by trivial bundles ), where the fields are sections of the bundle. Lagrangian physics is then described by a form on the jet bundle of , i.e. the bundle whose fibre over consists of the space describing the possible first derivatives of a section over that point.

More generally, a field theory gives a procedure for taking some space with structure – say a (pseudo-)Riemannian manifold – and produce a moduli space of fields. The Sigma models happen to be representable functors: for some , the representing object. A prestack is just any functor taking to a moduli space of fields. A stack is one which has a “descent condition”, which amounts to the condition of locality: knowing values on small neighbourhoods and how to glue them together determines values on larger neighborhoods.

The Yoneda lemma says that, for reasonable notions of “space”, the category from which we picked target spaces embeds into the category of stacks over (Riemannian manifolds, for instance) and that the embedding is faithful – so we should just think of this as a generalization of space. However, it’s a generalization we need, because gauge theories determine non-representable stacks. What’s more, the “space” of sections of one of these fibred stacks is also a stack, and this is what plays the role of the moduli space for gauge theory! For higher gauge theories, we will need higher stacks.

All of the above is the classical situation: the next issue is how to quantize such a theory. It involves a generalization of Geometric Quantization (GQ for short). Now a physicist who actually uses GQ will find this perspective weird, but it flows from just the same logic as the usual method.

In ordinary GQ, you have some classical system described by a phase space, a manifold equipped with a pre-symplectic 2-form . Intuitively, describes how the space, locally, can be split into conjugate variables. In the phase space for a particle in -space, these “position” and “momentum” variables, and ; many other systems have analogous conjugate variables. But what really matters is the form itself, or rather its cohomology class.

Then one wants to build a Hilbert space describing the quantum analog of the system, but in fact, you need a little more than to do this. The Hilbert space is a space of sections of some bundle whose sections look like copies of the complex numbers, called the “prequantum line bundle“. It needs to be equipped with a connection, whose curvature is a 2-form in the class of : in general, . (If is not symplectic, i.e. is degenerate, this implies there’s some symmetry on , in which case the line bundle had better be equivariant so that physically equivalent situations correspond to the same state). The easy case is the trivial bundle, so that we get a space of functions, like (for some measure compatible with ). In general, though, this function-space picture only makes sense locally in : this is why the choice of prequantum line bundle is important to the interpretation of the quantized theory.

Since the crucial geometric thing here is a bundle over the moduli space, when the space is a stack, and in the context of higher gauge theory, it’s natural to seek analogous constructions using higher bundles. This would involve, instead of a (pre-)symplectic 2-form , an -form called a (pre-)-plectic form (for an introductory look at this, see Chris Rogers’ paper on the case over manifolds). This will give a higher analog of the Hilbert space.

Now, maps between Hilbert spaces in QG come from Lagrangian correspondences – these might be maps of moduli spaces, but in general they consist of a “space of trajectories” equipped with maps into a space of incoming and outgoing configurations. This is a span of pre-symplectic spaces (equipped with pre-quantum line bundles) that satisfies some nice geometric conditions which make it possible to push a section of said line bundle through the correspondence. Since each prequantum line bundle can be seen as maps out of the configuration space into a classifying space (for , or in general an -group of phases), we get a square. The action functional is a cell that fills this square (see the end of 2.1.3 in Urs’ notes). This is a diagrammatic way to describe the usual GQ construction: the advantage is that it can then be repeated in the more general setting without much change.

This much is about as far as Urs got in his talk, but the notes go further, talking about how to extend this to infinity-stacks, and how the Dold-Kan correspondence tells us nicer descriptions of what we get when linearizing – since quantization puts us into an Abelian category.

I enjoyed these talks, although they were long and Urs came out looking pretty exhausted, because while I’ve seen several others on this program, this was the first time I’ve seen it discussed from the beginning, with a lot of motivation. This was presumably because we had a physically-minded part of the audience, whereas I’ve mostly seen these for mathematicians, and usually they come in somewhere in the middle and being more time-limited miss out some of the details and the motivation. The end result made it quite a natural development. Overall, very helpful!

 

Higher Gauge Theory in Edinburgh – Part II

Continuing from the previous post, we’ll take a detour in a different direction. The physics-oriented talks were by Martin Wolf, Sam Palmer, Thomas Strobl, and Patricia Ritter. Since my background in this subject isn’t particularly physics-y, I’ll do my best to summarize the ones that had obvious connections to other topics, but may be getting things wrong or unbalanced here…

Dirac Sigma Models

Thomas Strobl’s talk, “New Methods in Gauge Theory” (based on a whole series of papers linked to from the conference webpage), started with a discussion of of generalizing Sigma Models. Strobl’s talk was a bit high-level physics for me to do it justice, but I came away with the impression of a fairly large program that has several points of contact with more mathematical notions I’ll discuss later.

In particular, Sigma models are physical theories in which a field configuration on spacetime is a map into some target manifold, or rather , since we need a metric to integrate and find differentials. Given this, we can define the crucial physics ingredient, an action functional

where the are the differentials of the map into .

In string theory, is the world-sheet of a string and is ordinary spacetime. This generalizes the simpler example of a moving particle, where is just its worldline. In that case, minimizing the action functional above says that the particle moves along geodesics.

The big generalization introduced is termed a “Dirac Sigma Model” or DSM (the paper that introduces them is this one).

In building up to these DSM, a different generalization notes that if there is a group action that describes “rigid” symmetries of the theory (for Minkowski space we might pick the Poincare group, or perhaps the Lorentz group if we want to fix an origin point), then the action functional on the space is invariant in the direction of any of the symmetries. One can use this to reduce , by “gauging out” the symmetries to get a quotient , and get a corresponding to integrate over .

To generalize this, note that there’s an action groupoid associated with , and replace this with some other (Poisson) groupoid instead. That is, one thinks of the real target for a gauge theory not as , but the action groupoid , and then just considers replacing this with some generic groupoid that doesn’t necessarily arise from a group of rigid symmetries on some underlying . (In this regard, see the second post in this series, about Urs Schreiber’s talk, and stacks as classifying spaces for gauge theories).

The point here seems to be that one wants to get a nice generalization of this situation – in particular, to be able to go backward from to , to deal with the possibility that the quotient may be geometrically badly-behaved. Or rather, given , to find some of which it is a reduction, but which is better behaved. That means needing to be able to treat a Sigma model with symmetry information attached.

There’s also an infinitesimal version of this: locally, invariance means the Lie derivative of the action in the direction of any of the generators of the Lie algebra of – so called Killing vectors – is zero. So this equation can generalize to a case where there are vectors where the Lie derivative is zero – a so-called “generalized Killing equation”. They may not generate isometries, but can be treated similarly. What they do give, if you integrate these vectors, is a foliation of . The space of leaves is the quotient mentioned above.

The most generic situation Thomas discussed is when one has a Dirac structure on – this is a certain kind of subbundle of the tangent-plus-cotangent bundle over .

Supersymmetric Field Theories

Another couple of physics-y talks related higher gauge theory to some particular physics models, namely and supersymmetric field theories.

The first, by Martin Wolf, was called “Self-Dual Higher Gauge Theory”, and was rooted in generalizing some ideas about twistor geometry – here are some lecture notes by the same author, about how twistor geometry relates to ordinary gauge theory.

The idea of twistor geometry is somewhat analogous to the idea of a Fourier transform, which is ultimately that the same space of fields can be described in two different ways. The Fourier transform goes from looking at functions on a position space, to functions on a frequency space, by way of an integral transform. The Penrose-Ward transform, analogously, transforms a space of fields on Minkowski spacetime, satisfying one set of equations, to a set of fields on “twistor space”, satisfying a different set of equations. The theories represented by those fields are then equivalent (as long as the PW transform is an isomorphism).

The PW transform is described by a “correspondence”, or “double fibration” of spaces – what I would term a “span”, such that both maps are fibrations:

The general story of such correspondences is that one has some geometric data on , which we call – a set of functions, differential forms, vector bundles, cohomology classes, etc. They are pulled back to , and then “pushed forward” to by a direct image functor. In many cases, this is given by an integral along each fibre of the fibration , so we have an integral transform. The image of we call , and it consists of data satisfying, typically, some PDE’s.In the case of the PW transform, is complex projective 3-space and is the set of holomorphic principal bundles for some group ; is (complexified) Minkowski space and the fields are principal -bundles with connection. The PDE they satisfy is , where is the curvature of the bundle and is the Hodge dual). This means cohomology on twistor space (which classifies the bundles) is related self-dual fields on spacetime. One can also find that a point in corresponds to a projective line in , while a point in corresponds to a null plane in . (The space ).

Then the issue to to generalize this to higher gauge theory: rather than principal -bundles for a group, one is talking about a 2-group with connection. Wolf’s talk explained how there is a Penrose-Ward transform between a certain class of higher gauge theories (on the one hand) and an supersymmetric field theory (on the other hand). Specifically, taking , and to be (a subspace of) 6D projective space , there is a similar correspondence between certain holomorphic 2-bundles on and solutions to some self-dual field equations on (which can be seen as constraints on the curvature 3-form for a principal 2-bundle: the self-duality condition is why this only makes sense in 6 dimensions).

This picture generalizes to supermanifolds, where there are fermionic as well as bosonic fields. These turn out to correspond to a certain 6-dimensional supersymmetric field theory.

Then Sam Palmer gave a talk in which he described a somewhat similar picture for an supersymmetric theory. However, unlike the theory, this one gives, not a higher gauge theory, but something that superficially looks similar, but in fact is quite different. It ends up being a theory of a number of fields – form valued in three linked vector spaces

equipped with a bunch of maps that give the whole setup some structure. There is a collection of seven fields in groups (“multiplets”, in physics jargon) valued in each of these spaces. They satisfy a large number of identities. It somewhat resembles the higher gauge theory that corresponds to the case, so this situation gets called a “-gauge model”.

There are some special cases of such a setup, including Courant-Dorfman algebras and Lie 2-algebras. The talk gave quite a few examples of solutions to the equations that fall out. The overall conclusion is that, while there are some similarities between -gauge models and the way Higher Gauge Theory appears at the level of algebra-valued forms and the equations they must satisfy, there are some significant differences. I won’t try to summarize this in more depth, because (a) I didn’t follow the nitty-gritty technical details very well, and (b) it turns out to be not HGT, but some new theory which is less well understood at summary-level.

 

Higher Gauge Theory in Edinburgh – Part I

The main thing happening in my end of the world is that it’s relocated from Europe back to North America. I’m taking up a teaching postdoc position in the Mathematics and Computer Science department at Mount Allison University starting this month. However, amidst all the preparations and moving, I was also recently in Edinburgh, Scotland for a workshop on Higher Gauge Theory and Higher Quantization, where I gave a talk called 2-Group Symmetries on Moduli Spaces in Higher Gauge Theory. That’s what I’d like to write about this time.

Edinburgh is a beautiful city, though since the workshop was held at Heriot-Watt University, whose campus is outside the city itself, I only got to see it on the Saturday after the workshop ended. However, John Huerta and I spent a while walking around, and as it turned out, climbing a lot: first the Scott Monument, from which I took this photo down Princes Street:

And then up a rather large hill called Arthur’s Seat, in Holyrood Park next to the Scottish Parliament.

The workshop itself had an interesting mix of participants. Urs Schreiber gave the most mathematically sophisticated talk, and mine was also quite category-theory-minded. But there were also some fairly physics-minded talks that are interesting to me as well because they show the source of these ideas. In this first post, I’ll begin with my own, and continue with David Roberts’ talk on constructing an explicit string bundle. …

2-Group Symmetries of Moduli Spaces

My own talk, based on work with Roger Picken, boils down to a couple of observations about the notion of symmetry, and applies them to a discrete model in higher gauge theory. It’s the kind of model you might use if you wanted to do lattice gauge theory for a BF theory, or some other higher gauge theory. But the discretization is just a convenience to avoid having to deal with infinite dimensional spaces and other issues that don’t really bear on the central point.

Part of that point was described in a previous post: it has to do with finding a higher analog for the relationship between two views of symmetry: one is “global” (I found the physics-inclined part of the audience preferred “rigid”), to do with a group action on the entire space; the other is “local”, having to do with treating the points of the space as objects of a groupoid who show how points are related to each other. (Think of trying to describe the orbit structure of just the part of a group action that relates points in a little neighborhood on a manifold, say.)

In particular, we’re interested in the symmetries of the moduli space of connections (or, depending on the context, flat connections) on a space, so the symmetries are gauge transformations. Now, here already some of the physically-inclined audience objected that these symmetries should just be eliminated by taking the quotient space of the group action. This is based on the slogan that “only gauge-invariant quantities matter”. But this slogan has some caveats: in only applies to closed manifolds, for one. When there are boundaries, it isn’t true, and to describe the boundary we need something which acts as a representation of the symmetries. Urs Schreiber pointed out a well-known example: the Chern-Simons action, a functional on a certain space of connections, is not gauge-invariant. Indeed, the boundary terms that show up due to this not-invariance explain why there is a Wess-Zumino-Witt theory associated with the boundaries when the bulk is described by Chern-Simons.

Now, I’ve described a lot of the idea of this talk in the previous post linked above, but what’s new has to do with how this applies to moduli spaces that appear in higher gauge theory based on a 2-group . The points in these space are connections on a manifold . In particular, since a 2-group is a group object in categories, the transformation groupoid (which captures global symmetries of the moduli space) will be a double category. It turns out there is another way of seeing this double category by local descriptions of the gauge transformations.

In particular, general gauge transformations in HGT are combinations of two special types, described geometrically by -valued functions, or -valued 1-forms, where is the group of objects of , and is the group of morphisms based at . If we think of connections as functors from the fundamental 2-groupoid into , these correspond to pseudonatural transformations between these functors. The main point is that there are also two special types of these, called “strict”, and “costrict”. The strict ones are just natural transformations, where the naturality square commutes strictly. The costrict ones, also called ICONs (for “identity component oplax natural transformations” – see the paper by Steve Lack linked from the nlab page above for an explanation of “costrictness”). They assign the identity morphism to each object, but the naturality square commutes only up to a specified 2-cell. Any pseudonatural transformation factors into a strict and costrict part.

The point is that taking these two types of transformation to be the horizontal and vertical morphisms of a double category, we get something that very naturally arises by the action of a big 2-group of symmetries on a category. We also find something which doesn’t happen in ordinary gauge theory: that only the strict gauge transformations arise from this global symmetry. The costrict ones must already be the morphisms in the category being acted on. This category plays the role of the moduli space in the normal 1-group situation. So moving to 2-groups reveals that in general we should distinguish between global/rigid symmetries of the moduli space, which are strict gauge transformations, and costrict ones, which do not arise from the global 2-group action and should be thought of as intrinsic to the moduli space.

String Bundles

David Roberts gave a rather interesting talk called “Constructing Explicit String Bundles”. There are some notes for this talk here. The point is simply to give an explicit construction of a particular 2-group bundle. There is a lot of general abstract theory about 2-bundles around, and a fair amount of work that manipulates physically-motivated descriptions of things that can presumably be modelled with 2-bundles. There has been less work on giving a mathematically rigorous description of specific, concrete 2-bundles.

This one is of interest because it’s based on the String 2-group. Details are behind that link, but roughly the classifying space of (a homotopy 2-type) is fibred over the classifying space for (a 1-type). The exact map is determined by taking a pullback along a certain characteristic class (which is a map out of ). Saying “the” string 2-group is a bit of a misnomer, by the way, since such a 2-group exists for every simply connected compact Lie group . The group that’s involved here is a , the string 2-group associated to , the universal cover of the rotation group . This is the one that determines whether a given manifold can support a “string structure”. A string structure on , therefore, is a lift of a spin structure, which determines whether one can have a spin bundle over , hence consistently talk about a spin connection which gives parallel transport for spinor fields on . The string structure determines if one can consistently talk about a string-bundle over , and hence a 2-group connection giving parallel transport for strings.

In this particular example, the idea was to find, explicitly, a string bundle over Minkowski space – or its conformal compactification. In point of fact, this particular one is for $latek String(5)$, and is over 6-dimensional Minkowski space, whose compactification is . This particular is convenient because it’s possible to show abstractly that it has exactly one nontrivial class of string bundles, so exhibiting one gives a complete classification. The details of the construction are in the notes linked above. The technical details rely on the fact that we can coordinatize nicely using the projective quaternionic plane, but conceptually it relies on the fact that , and because of how the lifting works, this is also . This quotient means there’s a string bundle whose fibre is .

While this is only one string bundle, and not a particularly general situation, it’s nice to see that there’s a nice elegant presentation which gives such a bundle explicitly (by constructing cocycles valued in the crossed module associated to the string 2-group, which give its transition functions).

(Here endeth Part I of this discussion of the workshop in Edinburgh. Part II will talk about Urs Schreiber’s very nice introduction to Higher Geometric Quantization)

(This ends the first part of this update – the next will describe the physics-oriented talks, and the third will describe Urs Schreiber’s series on higher geometric quantization)

 

TQFT’s in Vienna – Part 2

To continue from the previous post…

Twisted Differential Cohomology

Ulrich Bunke gave a talk introducing differential cohomology theories, and Thomas Nikolaus gave one about a twisted version of such theories (unfortunately, perhaps in the wrong order). The idea here is that cohomology can give a classification of field theories, and if we don’t want the theories to be purely topological, we would need to refine this. A cohomology theory is a (contravariant) functorial way of assigning to any space , which we take to be a manifold, a -graded group: that is, a tower of groups of “cocycles”, one group for each , with some coboundary maps linking them. (In some cases, the groups are also rings) For example, the group of differential forms, graded by degree.

Cohomology theories satisfy some axioms – for example, the Mayer-Vietoris sequence has to apply whenever you cut a manifold into parts. Differential cohomology relaxes one axiom, the requirement that cohomology be a homotopy invariant of . Given a differential cohomology theory, one can impose equivalence relations on the differential cocycles to get a theory that does satisfy this axiom – so we say the finer theory is a “differential refinement” of the coarser. So, in particular, ordinary cohomology theories are classified by spectra (this is related to the Brown representability theorem), whereas the differential ones are represented by sheaves of spectra – where the constant sheaves represent the cohomology theories which happen to be homotopy invariants.

The “twisting” part of this story can be applied to either an ordinary cohomology theory, or a differential refinement of one (though this needs similarly refined “twisting” data). The idea is that, if is a cohomology theory, it can be “twisted” over by a map into the “Picard group” of . This is the group of invertible -modules (where an -module means a module for the cohomology ring assigned to ) – essentially, tensoring with these modules is what defines the “twisting” of a cohomology element.

An example of all this is twisted differential K-theory. Here the groups are of isomorphism classes of certain vector bundles over , and the twisting is particularly simple (the Picard group in the topological case is just ). The main result is that, while topological twists are classified by appropriate gerbes on (for K-theory, -gerbes), the differential ones are classified by gerbes with connection.

Fusion Categories

Scott Morrison gave a talk about Classifying Fusion Categories, the point of which was just to collect together a bunch of results constructing particular examples. The talk opens with a quote by Rutherford: “All science is either physics or stamp collecting” – that is, either about systematizing data and finding simple principles which explain it, or about collecting lots of data. This talk was unabashed stamp-collecting, on the grounds that we just don’t have a lot of data to systematically understand yet – and for that very reason I won’t try to summarize all the results, but the slides are well worth a look-over. The point is that fusion categories are very useful in constructing TQFT’s, and there are several different constructions that begin “given a fusion category “… and yet there aren’t all that many examples, and very few large ones, known.

Scott also makes the analogy that fusion categories are “noncommutative finite groups” – which is a little confusing, since not all finite groups are commutative anyway – but the idea is that the symmetric fusion categories are exactly the representation categories of finite groups. So general fusion categories are a non-symmetric generalization of such groups. Since classifying finite groups turned out to be difficult, and involve a laundry-list of sporadic groups, it shouldn’t be too surprising that understanding fusion categories (which, for the symmetric case, include the representation categories of all these examples) should be correspondingly tricky. Since, as he points out, we don’t have very many non-symmetric examples beyond rank 12 (analogous to knowing only finite groups with at most 12 elements), it’s likely that we don’t have a very good understanding of these categories in general yet.

There were a couple of talks – one during the workshop by Sonia Natale, and one the previous week by Sebastian Burciu, whom I also had the chance to talk with that week – about “Equivariantization” of fusion categories, and some fairly detailed descriptions of what results. The two of them have a paper on this which gives more details, which I won’t summarize – but I will say a bit about the construction.

An “equivariantization” of a category acted on by a group is supposed to be a generalization of the notion of the set of fixed points for a group acting on a set.  The category has objects which consist of an object which is fixed by the action of , together with an isomorphism for each , satisfying a bunch of unsurprising conditions like being compatible with the group operation. The morphisms are maps in between the objects, which form commuting squares for each . Their paper, and the talks, described how this works when is a fusion category – namely, is also a fusion category, and one can work out its fusion rules (i.e. monoidal structure). In some cases, it’s a “group theoretical” fusion category (it looks like for some group ) – or a weakened version of such a thing (it’s Morita equivalent to ).

A nice special case of this is if the group action happens to be trivial, so that every object of is a fixed point. In this case, is just the category of objects of equipped with a -action, and the intertwining maps between these. For example, if , then (in particular, a “group-theoretical fusion category”). What’s more, this construction is functorial in itself: given a subgroup , we get an adjoint pair of functors between and , which in our special case are just the induced-representation and restricted-representation functors for that subgroup inclusion. That is, we have a Mackey functor here. These generalize, however, to any fusion category , and to nontrivial actions of on . The point of their paper, then, is to give a good characterization of the categories that come out of these constructions.

Quantizing with Higher Categories

The last talk I’d like to describe was by Urs Schreiber, called Linear Homotopy Type Theory for Quantization. Urs has been giving evolving talks on this topic for some time, and it’s quite a big subject (see the long version of the notes above if there’s any doubt). However, I always try to get a handle on these talks, because it seems to be describing the most general framework that fits the general approach I use in my own work. This particular one borrows a lot from the language of logic (the “linear” in the title alludes to linear logic).

Basically, Urs’ motivation is to describe a good mathematical setting in which to construct field theories using ingredients familiar to the physics approach to “field theory”, namely… fields. (See the description of Kevin Walker’s talk.) Also, Lagrangian functionals – that is, the notion of a physical action. Constructing TQFT from modular tensor categories, for instance, is great, but the fields and the action seem to be hiding in this picture. There are many conceptual problems with field theories – like the mathematical meaning of path integrals, for instance. Part of the approach here is to find a good setting in which to locate the moduli spaces of fields (and the spaces in which path integrals are done). Then, one has to come up with a notion of quantization that makes sense in that context.

The first claim is that the category of such spaces should form a differentially cohesive infinity-topos which we’ll call . The “infinity” part means we allow morphisms between field configurations of all orders (2-morphisms, 3-morphisms, etc.). The “topos” part means that all sorts of reasonable constructions can be done – for example, pullbacks. The “differentially cohesive” part captures the sort of structure that ensures we can really treat these as spaces of the suitable kind: “cohesive” means that we have a notion of connected components around (it’s implemented by having a bunch of adjoint functors between spaces and points). The “differential” part is meant to allow for the sort of structures discussed above under “differential cohomology” – really, that we can capture geometric structure, as in gauge theories, and not just topological structure.

In this case, we take to have objects which are spectral-valued infinity-stacks on manifolds. This may be unfamiliar, but the main point is that it’s a kind of generalization of a space. Now, the sort of situation where quantization makes sense is: we have a space (i.e. -object) of field configurations to start, then a space of paths (this is WHERE “path-integrals” are defined), and a space of field configurations in the final system where we observe the result. There are maps from the space of paths to identify starting and ending points. That is, we have a span:

Now, in fact, these may all lie over some manifold, such as , the classifying space for -gerbes. That is, we don’t just have these “spaces”, but these spaces equipped with one of those pieces of cohomological twisting data discussed up above. That enters the quantization like an action (it’s WHAT you integrate in a path integral).

Aside: To continue the parallel, quantization is playing the role of a cohomology theory, and the action is the twist. I really need to come back and complete an old post about motives, because there’s a close analogy here. If quantization is a cohomology theory, it should come by factoring through a universal one. In the world of motives, where “space” now means something like “scheme”, the target of this universal cohomology theory is a mild variation on just the category of spans I just alluded to. Then all others come from some functor out of it.

Then the issue is what quantization looks like on this sort of scenario. The Atiyah-Singer viewpoint on TQFT isn’t completely lost here: quantization should be a functor into some monoidal category. This target needs properties which allow it to capture the basic “quantum” phenomena of superposition (i.e. some additivity property), and interference (some actual linearity over ). The target category Urs talked about was the category of -rings. The point is that these are just algebras that live in the world of spectra, which is where our spaces already lived. The appropriate target will depend on exactly what is.

But what Urs did do was give a characterization of what the target category should be LIKE for a certain construction to work. It’s a “pull-push” construction: see the link way above on Mackey functors – restriction and induction of representations are an example . It’s what he calls a “(2-monoidal, Beck-Chevalley) Linear Homotopy-Type Theory”. Essentially, this is a list of conditions which ensure that, for the two morphisms in the span above, we have a “pull” operation for some and left and right adjoints to it (which need to be related in a nice way – the jargon here is that we must be in a Wirthmuller context), satisfying some nice relations, and that everything is functorial.

The intuition is that if we have some way of getting a “linear gadget” out of one of our configuration spaces of fields (analogous to constructing a space of functions when we do canonical quantization over, let’s say, a symplectic manifold), then we should be able to lift it (the “pull” operation) to the space of paths. Then the “push” part of the operation is where the “path integral” part comes in: many paths might contribute to the value of a function (or functor, or whatever it may be) at the end-point of those paths, because there are many ways to get from A to B, and all of them contribute in a linear way.

So, if this all seems rather abstract, that’s because the point of it is to characterize very generally what has to be available for the ideas that appear in physics notions of path-integral quantization to make sense. Many of the particulars – spectra, -rings, infinity-stacks, and so on – which showed up in the example are in a sense just placeholders for anything with the right formal properties. So at the same time as it moves into seemingly very abstract terrain, this approach is also supposed to get out of the toy-model realm of TQFT, and really address the trouble in rigorously defining what’s meant by some of the standard practice of physics in field theory by analyzing the logical structure of what this practice is really saying. If it turns out to involve some unexpected math – well, given the underlying issues, it would have been more surprising if it didn’t.

It’s not clear to me how far along this road this program gets us, as far as dealing with questions an actual physicist would like to ask (for the most part, if the standard practice works as an algorithm to produce results, physicists seldom need to ask what it means in rigorous math language), but it does seem like an interesting question.

 

Higher Structures in China

Since the last post, I’ve been busily attending some conferences, as well as moving to my new job at the University of Hamburg, in the Graduiertenkolleg 1670, “Mathematics Inspired by String Theory and Quantum Field Theory”.  The week before I started, I was already here in Hamburg, at the conference they were organizing “New Perspectives in Topological Quantum Field Theory“.  But since I last posted, I was also at the 20th Oporto Meeting on Geometry, Topology, and Physics, as well as the third Higher Structures in China workshop, at Jilin University in Changchun.  Right now, I’d like to say a few things about some of the highlights of that workshop.

Higher Structures in China III

So last year I had a bunch of discussions I had with Chenchang Zhu and Weiwei Pan, who at the time were both in Göttingen, about my work with Jamie Vicary, which I wrote about last time when the paper was posted to the arXiv.  In that, we showed how the Baez-Dolan groupoidification of the Heisenberg algebra can be seen as a representation of Khovanov’s categorification.  Chenchang and Weiwei and I had been talking about how these ideas might extend to other examples, in particular to give nice groupoidifications of categorified Lie algebras and quantum groups.

That is still under development, but I was invited to give a couple of talks on the subject at the workshop.  It was a long trip: from Lisbon, the farthest-west of the main cities of (continental) Eurasia all the way to one of the furthest-East.   (Not quite the furthest, but Changchun is in the northeast of China, just a few hours north of Korea, and it took just about exactly 24 hours including stopovers to get there).  It was a long way to go for a three day workshop, but as there were also three days of a big excursion to Changbai Mountain, just on the border with North Korea, for hiking and general touring around.  So that was a sort of holiday, with 11 other mathematicians.  Here is me with Dany Majard, in a national park along the way to the mountains:

Here’s me with Alex Hoffnung, on Changbai Mountain (in the background is China):

And finally, here’s me a little to the left of the previous picture, where you can see into the volcanic crater.  The lake at the bottom is cut out of the picture, but you can see the crater rim, of which this particular part is in North Korea, as seen from China:

Well, that was fun!

Anyway, the format of the workshop involved some talks from foreigners and some from locals, with a fairly big local audience including a good many graduate students from Jilin University.  So they got a chance to see some new work being done elsewhere – mostly in categorification of one kind or another.  We got a chance to see a little of what’s being done in China, although not as much as we might have. I gather that not much is being done yet that fit the theme of the workshop, which was part of the reason to organize the workshop, and especially for having a session aimed specially at the graduate students.

Categorified Algebra

This is a sort of broad term, but certainly would include my own talk.  The essential point is to show how the groupoidification of the Heisenberg algebra is a representation of Khovanov’s categorification of the same algebra, in a particular 2-category.  The emphasis here is on the fact that it’s a representation in a 2-category whose objects are groupoids, but whose morphisms aren’t just functors, but spans of functors – that is, composites of functors and co-functors.  This is a pretty conservative weakening of “representations on categories” – but it lets one build really simple combinatorial examples.  I’ve discussed this general subject in recent posts, so I won’t elaborate too much.  The lecture notes are here, if you like, though – they have more detail than my previous post, but are less technical than the paper with Jamie Vicary.

Aaron Lauda gave a nice introduction to the program of categorifying quantum groups, mainly through the example of the special case , somewhat along the same lines as in his introductory paper on the subject.  The story which gives the motivation is nice: one has knot invariants such as the Jones polynomial, based on representations of groups and quantum groups.  The Jones polynomial can be categorified to give Khovanov homology (which assigns a complex to a knot, whose graded Euler characteristic is the Jones polynomial) – but also assigns maps of complexes to cobordisms of knots.  One then wants to categorify the representation theory behind it – to describe actions of, for instance, quantum on categories.  This starting point is nice, because it can work by just mimicking the construction of and representations in terms of weight spaces: one gets categories which correspond to the “weight spaces” (usually just vector spaces), and the and operators give functors between them, and so forth.

Finding examples of categories and functors with this structure, and satisfying the right relations, gives “categorified representations” of the algebra – the monoidal categories of diagrams which are the “categorifications of the algebra” then are seen as the abstraction of exactly which relations these are supposed to satisfy.  One such example involves flag varieties.  A flag, as one might eventually guess from the name, is a nested collection of subspaces in some -dimensional space.  A simple example is the Grassmannian , which is the space of all 1-dimensional subspaces of (i.e. the projective space ), which is of course an algebraic variety.  Likewise, , the space of all -dimensional subspaces of is a variety.  The flag variety consists of all pairs , of a -dimensional subspace of , inside a -dimensional subspace (the case calls to mind the reason for the name: a plane intersecting a given line resembles a flag stuck to a flagpole).  This collection is again a variety.  One can go all the way up to the variety of “complete flags”, (where is -dimenisonal), any point of which picks out a subspace of each dimension, each inside the next.

The way this relates to representations is by way of geometric representation theory. One can see those flag varieties of the form as relating the Grassmanians: there are projections and , which act by just ignoring one or the other of the two subspaces of a flag.  This pair of maps, by way of pulling-back and pushing-forward functions, gives maps between the cohomology rings of these spaces.  So one gets a sequence , and maps between the adjacent ones.  This becomes a representation of the Lie algebra.  Categorifying this, one replaces the cohomology rings with derived categories of sheaves on the flag varieties – then the same sort of “pull-push” operation through (derived categories of sheaves on) the flag varieties defines functors between those categories.  So one gets a categorified representation.

Heather Russell‘s talk, based on this paper with Aaron Lauda, built on the idea that categorified algebras were motivated by Khovanov homology.  The point is that there are really two different kinds of Khovanov homology – the usual kind, and an Odd Khovanov Homology, which is mainly different in that the role played in Khovanov homology by a symmetric algebra is instead played by an exterior (antisymmetric) algebra.  The two look the same over a field of characteristic 2, but otherwise different.  The idea is then that there should be “odd” versions of various structures that show up in the categorifications of (and other algebras) mentioned above.

One example is the fact that, in the “even” form of those categorifications, there is a natural action of the Nil Hecke algebra on composites of the generators.  This is an algebra which can be seen to act on the space of polynomials in commuting variables, , generated by the multiplication operators , and the “divided difference operators” based on the swapping of two adjacent variables.  The Hecke algebra is defined in terms of “swap” generators, which satisfy some -deformed variation of the relations that define the symmetric group (and hence its group algebra).   The Nil Hecke algebra is so called since the “swap” (i.e. the divided difference) is nilpotent: the square of the swap is zero.  The way this acts on the objects of the diagrammatic category is reflected by morphisms drawn as crossings of strands, which are then formally forced to satisfy the relations of the Nil Hecke algebra.

The ODD Nil Hecke algebra, on the other hand, is an analogue of this, but the are anti-commuting, and one has different relations satisfied by the generators (they differ by a sign, because of the anti-commutation).  This sort of “oddification” is then supposed to happen all over.  The main point of the talk was to to describe the “odd” version of the categorified representation defined using flag varieties.  Then the odd Nil Hecke algebra acts on that, analogously to the even case above.

Marco Mackaay gave a couple of talks about the web algebra, describing the results of this paper with Weiwei Pan and Daniel Tubbenhauer.  This is the analog of the above, for , describing a diagram calculus which accounts for representations of the quantum group.  The “web algebra” was introduced by Greg Kuperberg – it’s an algebra built from diagrams which can now include some trivalent vertices, along with rules imposing relations on these.  When categorifying, one gets a calculus of “foams” between such diagrams.  Since this is obviously fairly diagram-heavy, I won’t try here to reproduce what’s in the paper – but an important part of is the correspondence between webs and Young Tableaux, since these are labels in the representation theory of the quantum group – so there is some interesting combinatorics here as well.

Algebraic Structures

Some of the talks were about structures in algebra in a more conventional sense.

Jiang-Hua Lu: On a class of iterated Poisson polynomial algebras.  The starting point of this talk was to look at Poisson brackets on certain spaces and see that they can be found in terms of “semiclassical limits” of some associative product.  That is, the associative product of two elements gives a power series in some parameter (which one should think of as something like Planck’s constant in a quantum setting).  The “classical” limit is the constant term of the power series, and the “semiclassical” limit is the first-order term.  This gives a Poisson bracket (or rather, the commutator of the associative product does).  In the examples, the spaces where these things are defined are all spaces of polynomials (which makes a lot of explicit computer-driven calculations more convenient). The talk gives a way of constructing a big class of Poisson brackets (having some nice properties: they are “iterated Poisson brackets”) coming from quantum groups as semiclassical limits.  The construction uses words in the generating reflections for the Weyl group of a Lie group .

Li Guo: Successors and Duplicators of Operads – first described a whole range of different algebra-like structures which have come up in various settings, from physics and dynamical systems, through quantum field theory, to Hopf algebras, combinatorics, and so on.  Each of them is some sort of set (or vector space, etc.) with some number of operations satisfying some conditions – in some cases, lots of operations, and even more conditions.  In the slides you can find several examples – pre-Lie and post-Lie algebras, dendriform algebras, quadri- and octo-algebras, etc. etc.  Taken as a big pile of definitions of complicated structures, this seems like a terrible mess.  The point of the talk is to point out that it’s less messy than it appears: first, each definition of an algebra-like structure comes from an operad, which is a formal way of summing up a collection of operations with various “arities” (number of inputs), and relations that have to hold.  The second point is that there are some operations, “successor” and “duplicator”, which take one operad and give another, and that many of these complicated structures can be generated from simple structures by just these two operations.  The “successor” operation for an operad introduces a new product related to old ones – for example, the way one can get a Lie bracket from an associative product by taking the commutator.  The “duplicator” operation takes existing products and introduces two new products, whose sum is the previous one, and which satisfy various nice relations.  Combining these two operations in various ways to various starting points yields up a plethora of apparently complicated structures.

Dany Majard gave a talk about algebraic structures which are related to double groupoids, namely double categories where all the morphisms are invertible.  The first part just defined double categories: graphically, one has horizontal and vertical 1-morphisms, and square 2-morphsims, which compose in both directions.  Then there are several special degenerate cases, in the same way that categories have as degenerate cases (a) sets, seen as categories with only identity morphisms, and (b) monoids, seen as one-object categories.  Double categories have ordinary categories (and hence monoids and sets) as degenerate cases.  Other degenerate cases are 2-categories (horizontal and vertical morphisms are the same thing), and therefore their own special cases, monoidal categories and symmetric monoids.  There is also the special degenerate case of a double monoid (and the extra-special case of a double group).  (The slides have nice pictures showing how they’re all degenerate cases).  Dany then talked about some structure of double group(oids) – and gave a list of properties for double groupoids, (such as being “slim” – having at most one 2-cell per boundary configuration – as well as two others) which ensure that they’re equivalent to the semidirect product of an abelian group with the “bicrossed product”  of two groups and (each of which has to act on the other for this to make sense).  He gave the example of the Poincare double group, which breaks down as a triple bicrossed product by the Iwasawa decomposition:

( is certain group of matrices).  So there’s a unique double group which corresponds to it – it has squares labelled by , and the horizontial and vertical morphisms by elements of and respectively.  Dany finished by explaining that there are higher-dimensional analogs of all this – -tuple categories can be defined recursively by internalization (“internal categories in -tuple-Cat”).  There are somewhat more sophisticated versions of the same kind of structure, and finally leading up to a special class of -tuple groups.  The analogous theorem says that a special class of them is just the same as the semidirect product of an abelian group with an -fold iterated bicrossed product of groups.

Also in this category, Alex Hoffnung talked about deformation of formal group laws (based on this paper with various collaborators).  FGL’s are are structures with an algebraic operation which satisfies axioms similar to a group, but which can be expressed in terms of power series.  (So, in particular they have an underlying ring, for this to make sense).  In particular, the talk was about formal group algebras – essentially, parametrized deformations of group algebras – and in particular for Hecke Algebras.  Unfortunately, my notes on this talk are mangled, so I’ll just refer to the paper.

Physics

I’m using the subject-header “physics” to refer to those talks which are most directly inspired by physical ideas, though in fact the talks themselves were mathematical in nature.

Fei Han gave a series of overview talks intorducing “Equivariant Cohomology via Gauged Supersymmetric Field Theory”, explaining the Stolz-Teichner program.  There is more, using tools from differential geometry and cohomology to dig into these theories, but for now a summary will do.  Essentially, the point is that one can look at “fields” as sections of various bundles on manifolds, and these fields are related to cohomology theories.  For instance, the usual cohomology of a space is a quotient of the space of closed forms (so the cohomology, , is a quotient of the space of closed -forms – the quotient being that forms differing by a coboundary are considered the same).  There’s a similar construction for the -theory , which can be modelled as a quotient of the space of vector bundles over .  Fei Han mentioned topological modular forms, modelled by a quotient of the space of “Fredholm bundles” – bundles of Banach spaces with a Fredholm operator around.

The first two of these examples are known to be related to certain supersymmetric topological quantum field theories.  Now, a TFT is a functor into some kind of vector spaces from a category of -dimensional manifolds and -dimensional cobordisms

Intuitively, it gives a vector space of possible fields on the given space and a linear map on a given spacetime.  A supersymmetric field theory is likewise a functor, but one changes the category of “spacetimes” to have both bosonic and fermionic dimension.  A normal smooth manifold is a ringed space , since it comes equipped with a sheaf of rings (each open set has an associated ring of smooth functions, and these glue together nicely).  Supersymmetric theories work with manifolds which change this sheaf – so a -dimensional space has the sheaf of rings where one introduces some new antisymmetric coordinate functions , the “fermionic dimensions”:

Then a supersymmetric TFT is a functor:

(where is the category of supersymmetric topological vector spaces – defined similarly).  The connection to cohomology theories is that the classes of such field theories, up to a notion of equivalence called “concordance”, are classified by various cohomology theories.  Ordinary cohomology corresponds then to -dimensional extended TFT (that is, with 0 bosonic and 1 fermionic dimension), and -theory to a -dimensional extended TFT.  The Stoltz-Teichner Conjecture is that the third example (topological modular forms) is related in the same way to a -dimensional extended TFT – so these are the start of a series of cohomology theories related to various-dimension TFT’s.

Last but not least, Chris Rogers spoke about his ideas on “Higher Geometric Quantization”, on which he’s written a number of papers.  This is intended as a sort of categorification of the usual ways of quantizing symplectic manifolds.  I am still trying to catch up on some of the geometry This is rooted in some ideas that have been discussed by Brylinski, for example.  Roughly, the message here is that “categorification” of a space can be thought of as a way of acting on the loop space of a space.  The point is that, if points in a space are objects and paths are morphisms, then a loop space shifts things by one categorical level: its points are loops in , and its paths are therefore certain 2-morphisms of .  In particular, there is a parallel to the fact that a bundle with connection on a loop space can be thought of as a gerbe on the base space.  Intuitively, one can “parallel transport” things along a path in the loop space, which is a surface given by a path of loops in the original space.  The local description of this situation says that a 1-form (which can give transport along a curve, by integration) on the loop space is associated with a 2-form (giving transport along a surface) on the original space.

Then the idea is that geometric quantization of loop spaces is a sort of higher version of quantization of the original space. This “higher” version is associated with a form of higher degree than the symplectic (2-)form used in geometric quantization of .   The general notion of n-plectic geometry, where the usual symplectic geometry is the case , involves a -form analogous to the usual symplectic form.  Now, there’s a lot more to say here than I properly understand, much less can summarize in a couple of paragraphs.  But the main theorem of the talk gives a relation between n-plectic manifolds (i.e. ones endowed with the right kind of form) and Lie n-algebras built from the complex of forms on the manifold.  An important example (a theorem of Chris’ and John Baez) is that one has a natural example of a 2-plectic manifold in any compact simple Lie group together with a 3-form naturally constructed from its Maurer-Cartan form.

At any rate, this workshop had a great proportion of interesting talks, and overall, including the chance to see a little more of China, was a great experience!

 

Representations and Categories – Part II (Erlangen)

Well, as promised in the previous post, I’d like to give a summary of some of what was discussed at the conference I attended (quite a while ago now, late last year) in Erlangen, Germany.  I was there also to visit Derek Wise, talking about a project we’ve been working on for some time.

(I’ve also significantly revised this paper about Extended TQFT since then, and it now includes some stuff which was the basis of my talk at Erlangen on cohomological twisting of the category .  I’ll get to that in the next post.  Also coming up, I’ll be describing some new things I’ve given some talks about recently which relate the Baez-Dolan groupoidification program to Khovanov-Lauda categorification of algebras – at least in one example, hopefully in a way which will generalize nicely.)

In the meantime, there were a few themes at the conference which bear on the Extended TQFT project in various ways, so in this post I’ll describe some of them.  (This isn’t an exhaustive description of all the talks: just of a selection of illustrative ones.)

---

Categories with Structures

A few talks were mainly about facts regarding the sorts of categories which get used in field theory contexts.  One important type, for instance, are fusion categories is a monoidal category which is enriched in vector spaces, generated by simple objects, and some other properties: essentially, monoidal 2-vector spaces.  The basic example would be categories of representations (of groups, quantum groups, algebras, etc.), but fusion categories are an abstraction of (some of) their properties.  Many of the standard properties are described and proved in this paper by Etingof, Nikshych, and Ostrik, which also poses one of the basic conjectures, the “ENO Conjecture”, which was referred to repeatedly in various talks.  This is the guess that every fusion category can be given a “pivotal” structure: an isomorphism from to .  It generalizes the theorem that there’s always such an isomorphism into .  More on this below.

Hendryk Pfeiffer talked about a combinatorial way to classify fusion categories in terms of certain graphs (see this paper here).  One way I understand this idea is to ask how much this sort of category really does generalize categories of representations, or actually comodules.  One starting point for this is the theorem that there’s a pair of functors between certain monoidal categories and weak Hopf algebras.  Specifically, the monoidal categories are , which consists of monoidal categories equipped with a forgetful functor into .  Then from this one can get (via a coend), a weak Hopf algebra over the base field (in the category ).  From a weak Hopf algebra , one can get back such a category by taking all the modules of .  These two processes form an adjunction: they’re not inverses, but we have maps between the two composites and the identity functors.

The new result Hendryk gave is that if we restrict our categories over to be abelian, and the functors between them to be linear, faithful, and exact (that is, roughly, that we’re talking about concrete monoidal 2-vector spaces), then this adjunction is actually an equivalence: so essentially, all such categories may as well be module categories for weak Hopf algebras.  Then he gave a characterization of these in terms of the “dimension graph” (in fact a quiver) for , where is one of the monoidal generators of .  The vertices of are labelled by the irreducible representations (i.e. set of generators of the category), and there’s a set of edges labelled by a basis of .  Then one can carry on and build a big graded algebra whose -graded part consists of length- paths in .  Then the point is that the weak Hopf algebra of which is (up to isomorphism) the module category will be a certain quotient of (after imposing some natural relations in a systematic way).

The point, then, is that the sort of categories mostly used in this area can be taken to be representation categories, but in general only of these weak Hopf algebras: groups and ordinary algebras are special cases, but they show up naturally for certain kinds of field theory.

Tensor Categories and Field Theories

There were several talks about the relationship between tensor categories of various sorts and particular field theories.  The idea is that local field theories can be broken down in terms of some kind of n-category: -dimensional regions get labelled by categories, -D boundaries between regions, or “defects”, are labelled by functors between the categories (with the idea that this shows how two different kinds of field can couple together at the defect), and so on (I think the highest-dimension that was discussed explicitly involved 3-categories, so one has junctions between defects, and junctions between junctions, which get assigned some higher-morphism data).  Alteratively, there’s the dual picture where categories are assigned to points, functors to 1-manifolds, and so on.  (This is just Poincaré duality in the case where the manifolds come with a decomposition into cells, which they often are if only for convenience).

Victor Ostrik gave a pair of talks giving an overview role tensor categories play in conformal field theory.  There’s too much material here to easily summarize, but the basics go like this: CFTs are field theories defined on cobordisms that have some conformal structure (i.e. notion of angles, but not distance), and on the algebraic side they are associated with vertex algebras (some useful discussion appears on mathoverflow, but in this context they can be understood as vector spaces equipped with exactly the algebraic operations needed to model cobordisms with some local holomorphic structure).

In particular, the irreducible representations of these VOA’s determine the “conformal blocks” of the theory, which tell us about possible correlations between observables (self-adjoint operators).  A VOA is “rational” if the category is semisimple (i.e. generated as finite direct sums of these conformal blocks).  For good VOA’s, will be a modular tensor category (MTC), which is a fusion category with a duality, braiding, and some other strucutre (see this for more).   So describing these gives us a lot of information about what CFT’s are possible.

The full data of a rational CFT are given by a vertex algebra, and a module category : that is, a fusion category is a sort of categorified ring, so it can act on as an ring acts on a module.  It turns out that choosing an is equivalent to finding a certain algebra (i.e. algebra object) , a “Lagrangian algebra” inside the centre of .  The Drinfel’d centre of a monoidal category is a sort of free way to turn a monoidal category into a braided one: but concretely in this case it just looks like .  Knowing the isomorphism class determines a “modular invariant”.  It gets “physics” meaning from how it’s equipped with an algebra structure (which can happen in more than one way), but in any case has an underlying vector space, which becomes the Hilbert space of states for the conformal field theory, which the VOA acts on in the natural way.

Now, that was all conformal field theory.  Christopher Douglas described some work with Chris Schommer-Pries and Noah Snyder about fusion categories and structured topological field theories.  These are functors out of cobordism categories, the most important of which are -categories, where the objects are points, morphisms are 1D cobordisms, and so on up to -morphisms which are -dimensional cobordisms.  To keep things under control, Chris Douglas talked about the case , which is where , and a “local” field theory is a 3-functor for some 3-category .  Now, the (Baez-Dolan) Cobordism Hypothesis, which was proved by Jacob Lurie, says that is, in a suitable sense, the free symmetric monoidal 3-category with duals.  What this amounts to is that a local field theory whose target 3-category is is “just” a dualizable object of .

The handy example which links this up to the above is when has objects which are tensor categories, morphisms which are bimodule categories (i.e. categories acted), 2-morphisms which are functors, and 3-morphisms which are natural transformations.  Then the issue is to classify what kind of tensor categories these objects can be.

The story is trickier if we’re talking about, not just topological cobordisms, but ones equipped with some kind of structure regulated by a structure group (for instance, orientation by , spin structure by its universal cover , and so on).  This means the cobordisms come equipped with a map into .  They take as the starting point, and then consider groups with a map to , and require that the map into is a lift of the map to .  Then one gets that a structured local field theory amounts to a dualizable objects of with a homotopy-fixed point for some -action – and this describes what gets assigned to the point by such a field theory.  What they then show is a correspondence between and classes of categories.  For instance, fusion categories are what one gets by imposing that the cobordisms be oriented.

Liang Kong talked about “Topological Orders and Tensor Categories”, which used the Levin-Wen models, from condensed matter phyiscs.  (Benjamin Balsam also gave a nice talk describing these models and showing how they’re equivalent to the Turaev-Viro and Kitaev models in appropriate cases.  Ingo Runkel gave a related talk about topological field theories with “domain walls”.).  Here, the idea of a “defect” (and topological order) can be understood very graphically: we imagine a 2-dimensional crystal lattice (of atoms, say), and the defect is a 1-dimensional place where the two lattices join together, with the internal symmetry of each breaking down at the boundary.  (For example, a square lattice glued where the edges on one side are offset and meet the squares on the other side in the middle of a face, as you typically see in a row of bricks – the slides linked above have some pictures).  The Levin-Wen models are built using a hexagonal lattice, starting with a tensor category with several properties: spherical (there are dualities satisfying some relations), fusion, and unitary: in fact, historically, these defining properties were rediscovered independently here as the requirement for there to be excitations on the boundary which satisfy physically-inspired consistency conditions.

These abstract the properties of a category of representations.  A generalization of this to “topological orders” in 3D or higher is an extended TFT in the sense mentioned just above: they have a target 3-category of tensor categories, bimodule categories, functors and natural transformations.  The tensor categories (say, , , etc.) get assigned to the bulk regions; to “domain walls” between different regions, namely defects between lattices, we assign bimodule categories (but, for instance, to a line within a region, we get understood as a -bimodule); then to codimension 2 and 3 defects we attach functors and natural transformations.  The algebra for how these combine expresses the ways these topological defects can go together.  On a lattice, this is an abstraction of a spin network model, where typically we have just one tensor category applied to the whole bulk, namely the representations of a Lie group (say, a unitary group).  Then we do calculations by breaking down into bases: on codimension-1 faces, these are simple objects of ; to vertices we assign a Hom space (and label by a basis for intertwiners in the special case); and so on.

Thomas Nickolaus spoke about the same kind of -equivariant Dijkgraaf-Witten models as at our workshop in Lisbon, so I’ll refer you back to my earlier post on that.  However, speaking of equivariance and group actions:

Michael Müger  spoke about “Orbifolds of Rational CFT’s and Braided Crossed -Categories” (see this paper for details).  This starts with that correspondence between rational CFT’s (strictly, rational chiral CFT’s) and modular categories .  (He takes to be the name of the CFT).  Then we consider what happens if some finite group acts on (if we understand as a functor, this is an action by natural transformations; if as an algebra, then ).  This produces an “orbifold theory” (just like a finite group action on a manifold produces an orbifold), which is the “-fixed subtheory” of , by taking -fixed points for every object, and is also a rational CFT.  But that means it corresponds to some other modular category , so one would like to know what category this is.

A natural guess might be that it’s , where is a “weak fixed-point” category that comes from a weak group action on a category .  Objects of are pairs where and is a specified isomorphism.  (This is a weak analog of , the set of fixed points for a group acting on a set).  But this guess is wrong – indeed, it turns out these categories have the wrong dimension (which is defined because the modular category has a trace, which we can sum over generating objects).  Instead, the right answer, denoted by , is the -fixed part of some other category.  It’s a braided crossed -category: one with a grading by , and a -action that gets along with it.  The identity-graded part of is just the original .

State Sum Models

This ties in somewhat with at least some of the models in the previous section.  Some of these were somewhat introductory, since many of the people at the conference were coming from a different background.  So, for instance, to begin the workshop, John Barrett gave a talk about categories and quantum gravity, which started by outlining the historical background, and the development of state-sum models.  He gave a second talk where he began to relate this to diagrams in Gray-categories (something he also talked about here in Lisbon in February, which I wrote about then).  He finished up with some discussion of spherical categories (and in particular the fact that there is a Gray-category of spherical categories, with a bunch of duals in the suitable sense).  This relates back to the kind of structures Chris Douglas spoke about (described above, but chronologically right after John).  Likewise, Winston Fairbairn gave a talk about state sum models in 3D quantum gravity – the Ponzano Regge model and Turaev-Viro model being the focal point, describing how these work and how they’re constructed.  Part of the point is that one would like to see that these fit into the sort of framework described in the section above, which for PR and TV models makes sense, but for the fancier state-sum models in higher dimensions, this becomes more complicated.

Higher Gauge Theory

There wasn’t as much on this topic as at our own workshop in Lisbon (though I have more remarks on higher gauge theory in one post about it), but there were a few entries.  Roger Picken talked about some work with Joao Martins about a cubical formalism for parallel transport based on crossed modules, which consist of a group and abelian group , with a map and an action of on satisfying some axioms.  They can represent categorical groups, namely group objects in (equivalently, categories internal to ), and are “higher” analogs of groups with a set of elements.  Roger’s talk was about how to understand holonomies and parallel transports in this context.  So, a “connection” lets on transport things with -symmetries along paths, and with -symmetries along surfaces.  It’s natural to describe this with squares whose edges are labelled by -elements, and faces labelled by -elements (which are the holonomies).  Then the “cubical approach” means that we can describe gauge transformations, and higher gauge transformations (which in one sense are the point of higher gauge theory) in just the same way: a gauge transformation which assigns -values to edges and -values to vertices can be drawn via the holonomies of a connection on a cube which extends the original square into 3D (so the edges become squares, and so get -values, and so on).  The higher gauge transformations work in a similar way.  This cubical picture gives a good way to understand the algebra of how gauge transformations etc. work: so for instance, gauge transformations look like “conjugation” of a square by four other squares – namely, relating the front and back faces of a cube by means of the remaining faces.  Higher gauge transformations can be described by means of a 4D hypercube in an analogous way, and their algebraic properties have to do with the 2D faces of the hypercube.

Derek Wise gave a short talk outlining his recent paper with John Baez in which they show that it’s possible to construct a higher gauge theory based on the Poincare 2-group which turns out to have fields, and dynamics, which are equivalent to teleparallel gravity, a slightly unusal theory which nevertheless looks in practice just like General Relativity.  I discussed this in a previous post.

So next time I’ll talk about the new additions to my paper on ETQFT which were the basis of my talk, which illustrates a few of the themes above.

 

Two Workshops on Representations and Categories – Part I

So I’ve been travelling a lot in the last month, spending more than half of it outside Portugal. I was in Ottawa, Canada for a Fields Institute workshop, “Categorical Methods in Representation Theory“. Then a little later I was in Erlangen, Germany for one called “Categorical and Representation-Theoretic Methods in Quantum Geometry and CFT“. Despite the similar-sounding titles, these were on fairly different themes, though Marco Mackaay was at both, talking about categorifying the -Schur algebra by diagrams.  I’ll describe the meetings, but for now I’ll start with the first.  Next post will be a summary of the second.

The Ottawa meeting was organized by Alistair Savage, and Alex Hoffnung (like me, a former student of John Baez). Alistair gave a talk here at IST over the summer about a -deformation of Khovanov’s categorification of the Heisenberg Algebra I discussed in an earlier entry. A lot of the discussion at the workshop was based on the Khovanov-Lauda program, which began with categorifying quantum version of the classical Lie groups, and is now making lots of progress in the categorification of algebras, representation theory, and so on.

The point of this program is to describe “categorifications” of particular algebras. This means finding monoidal categories with the property that when you take the Grothendieck ring (the ring of isomorphism classes, with a multiplication given by the monoidal structure), you get back the integral form of some algebra. (And then recover the original by taking the tensor over with ). The key thing is how to represent the algebra by generators and relations. Since free monoidal categories with various sorts of structures can be presented as categories of string diagrams, it shouldn’t be surprising that the categories used tend to have objects that are sequences (i.e. monoidal products) of dots with various sorts of labelling data, and morphisms which are string diagrams that carry those labels on strands (actually, usually they’re linear combinations of such diagrams, so everything is enriched in vector spaces). Then one imposes relations on the “free” data given this way, by saying that the diagrams are considered the same morphism if they agree up to some local moves. The whole problem then is to find the right generators (labelling data) and relations (local moves). The result will be a categorification of a given presentation of the algebra you want.

So for instance, I was interested in Sabin Cautis and Anthony Licata‘s talks connected with this paper, “Heisenberg Categorification And Hilbert Schemes”. This is connected with a generalization of Khovanov’s categorification linked above, to include a variety of other algebras which are given a similar name. The point is that there’s such a “Heisenberg algebra” associated to different subgroups , which in turn are classified by Dynkin diagrams. The vertices of these Dynkin diagrams correspond to some generators of the Heisenberg algebra, and one can modify Khovanov’s categorification by having strands in the diagram calculus be labelled by these vertices. Rules for local moves involving strands with different labels will be governed by the edges of the Dynkin diagram. Their paper goes on to describe how to represent these categorifications on certain categories of Hilbert schemes.

Along the same lines, Aaron Lauda gave a talk on the categorification of the NilHecke algebra. This is defined as a subalgebra of endomorphisms of , generated by multiplications (by the ) and the divided difference operators . There are different from the usual derivative operators: in place of the differences between values of a single variable, they measure how a function behaves under the operation which switches variables and (that is, the reflection in the hyperplane where ). The point is that just like differentiation, this operator – together with multiplication – generates an algebra in . Aaron described how to categorify this presentation of the NilHecke algebra with a string-diagram calculus.

So anyway, there were a number of talks about the explosion of work within this general program – for instance, Marco Mackaay’s which I mentioned, as well as that of Pedro Vaz about the same project. One aspect of this program is that the relatively free “string diagram categories” are sometimes replaced with categories where the objects are bimodules and morphisms are bimodule homomorphisms. Making the relationship precise is then a matter of proving these satisfy exactly the relations on a “free” category which one wants, but sometimes they’re a good setting to prove one has a nice categorification. Thus, Ben Elias and Geordie Williamson gave two parts of one talk about “Soergel Bimodules and Kazhdan-Lusztig Theory” (see a blog post by Ben Webster which gives a brief intro to this notion, including pointing out that Soergel bimodules give a categorification of the Hecke algebra).

One of the reasons for doing this sort of thing is that one gets invariants for manifolds from algebras – in particular, things like the Jones polynomial, which is related to the Temperley-Lieb algebra. A categorification of it is Khovanov homology (which gives, for a manifold, a complex, with the property that the graded Euler characteristic of the complex is the Jones polynomial). The point here is that categorifying the algebra lets you raise the dimension of the kind of manifold your invariants are defined on.

So, for instance, Scott Morrison described “Invariants of 4-Manifolds from Khonanov Homology“.  This was based on a generalization of the relationship between TQFT’s and planar algebras.  The point is, planar algebras are described by the composition of diagrams of the following form: a big circle, containing some number of small circles.  The boundaries of each circle are labelled by some number of marked points, and the space between carries curves which connect these marked points in some way.  One composes these diagrams by gluing big circles into smaller circles (there’s some further discussion here including a picture, and much more in this book here).  Scott Morrison described these diagrams as “spaghetti and meatball” diagrams.  Planar algebras show up by associating a vector spaces to “the” circle with marked points, and linear maps to each way (up to isotopy) of filling in edges between such circles.  One can think of the circles and marked-disks as a marked-cobordism category, and so a functorial way of making these assignments is something like a TQFT.  It also gives lots of vector spaces and lots of linear maps that fit together in a particular way described by this category of marked cobordisms, which is what a “planar algebra” actually consists of.  Clearly, these planar algebras can be used to get some manifold invariants – namely the “TQFT” that corresponds to them.

Scott Morrison’s talk described how to get invariants of 4-dimensional manifolds in a similar way by boosting (almost) everything in this story by 2 dimensions.  You start with a 4-ball, whose boundary is a 3-sphere, and excise some number of 4-balls (with 3-sphere boundaries) from the interior.  Then let these 3D boundaries be “marked” with 1-D embedded links (think “knots” if you like).  These 3-spheres with embedded links are the objects in a category.  The morphisms are 4-balls which connect them, containing 2D knotted surfaces which happen to intersect the boundaries exactly at their embedded links.  By analogy with the image of “spaghetti and meatballs”, where the spaghetti is a collection of 1D marked curves, Morrison calls these 4-manifolds with embedded 2D surfaces “lasagna diagrams” (which generalizes to the less evocative case of “ pasta diagrams”, where we’ve just mentioned the and cases, with -dimensional “pasta” embedded in -dimensional balls).  Then the point is that one can compose these pasta diagrams by gluing the 4-balls along these marked boundaries.  One then gets manifold invariants from these sorts of diagrams by using Khovanov homology, which assigns to

Ben Webster talked about categorification of Lie algebra representations, in a talk called “Categorification, Lie Algebras and Topology“. This is also part of categorifying manifold invariants, since the Reshitikhin-Turaev Invariants are based on some monoidal category, which in this case is the category of representations of some algebra.  Categorifying this to a 2-category gives higher-dimensional equivalents of the RT invariants.  The idea (which you can check out in those slides) is that this comes down to describing the analog of the “highest-weight” representations for some Lie algebra you’ve already categorified.

The Lie theory point here, you might remember, is that representations of Lie algebras can be analyzed by decomposing them into “weight spaces” , associated to weights (where is the base field, which we can generally assume is ).  Weights turn Lie algebra elements into scalars, then.  So weight spaces generalize eigenspaces, in that acting by any element on a “weight vector” amounts to multiplying by .  (So that is an eigenvector for each , but the eigenvalue depends on , and is given by the weight.)  A weight can be the “highest” with respect to a natural order that can be put on weights ( if the difference is a nonnegative combination of simple weights).  Then a “highest weight representation” is one which is generated under the action of by a single weight vector , the “highest weight vector”.

The point of the categorification is to describe the representation in the same terms.  First, we introduce a special strand (which Ben Webster draws as a red strand) which represents the highest weight vector.  Then we say that the category that stands in for the highest weight representation is just what we get by starting with this red strand, and putting all the various string diagrams of the categorification of next to it.  One can then go on to talk about tensor products of these representations, where objects are found by amalgamating several such diagrams (with several red strands) together.  And so on.  These categorified representations are then supposed to be usable to give higher-dimensional manifold invariants.

Now, the flip side of higher categories that reproduce ordinary representation theory would be the representation theory of higher categories in their natural habitat, so to speak. Presumably there should be a fairly uniform picture where categorifications of normal representation theory will be special cases of this. Vlodymyr Mazorchuk gave an interesting talk called 2-representations of finitary 2-categories.  He gave an example of one of the 2-categories that shows up a lot in these Khovanov-Lauda categorifications, the 2-category of Soergel Bimodules mentioned above.  This has one object, which we can think of as a category of modules over the algebra (where I  is some ideal of homogeneous symmetric polynomials).  The morphisms are endofunctors of this category, which all amount to tensoring with certain bimodules – the irreducible ones being the Soergel bimodules.  The point of the talk was to explain the representations of 2-categories – that is, 2-functors from into some “classical” 2-category.  Examples would be 2-categories like “2-vector spaces”, or variants on it.  The examples he gave: (1) [small fully additive -linear categories], (2) the full subcategory of it with finitely many indecomposible elements, (3) [categories equivalent to module categories of finite dimensional associative -algebras].  All of these have some claim to be a 2-categorical analog of [vector spaces].  In general, Mazorchuk allowed representations of “FIAT” categories: Finitary (Two-)categories with Involutions and Adjunctions.

Part of the process involved getting a “multisemigroup” from such categories: a set with an operation which takes pairs of elements, and returns a subset of , satisfying some natural associativity condition.  (Semigroups are the case where the subset contains just one element – groups are the case where furthermore the operation is invertible).  The idea is that FIAT categories have some set of generators – indecomposable 1-morphisms – and that the multisemigroup describes which indecomposables show up in a composite.  (If we think of the 2-category as a monoidal category, this is like talking about a decomposition of a tensor product of objects).  So, for instance, for the 2-category that comes from the monoidal category of modules, we get the semigroup of nonnegative integers.  For the Soergel bimodule 2-category, we get the symmetric group.  This sort of thing helps characterize when two objects are equivalent, and in turn helps describe 2-representations up to some equivalence.  (You can find much more detail behind the link above.)

On the more classical representation-theoretic side of things, Joel Kamnitzer gave a talk called “Spiders and Buildings”, which was concerned with some geometric and combinatorial constructions in representation theory.  These involved certain trivalent planar graphs, called “webs”, whose edges carry labels between 1 and .  They’re embedded in a disk, and the outgoing edges, with labels determine a representation space for a group , say , namely the tensor product of a bunch of wedge products, , where acts on as usual.  Then a web determines an invariant vector in this space.  This comes about by having invariant vectors for each vertex (the basic case where ), and tensoring them together.  But the point is to interpret this construction geometrically.  This was a bit outside my grasp, since it involves the Langlands program and the geometric Satake correspondence, neither of which I know much of anything about, but which give geometric/topological ways of constructing representation categories.  One thing I did pick up is that it uses the “Langlands dual group” of to get a certain metric space called .  Then there’s a correspondence between the category of representations of and the category of (perverse, constructible) sheaves on this space.  This correspondence can be used to describe the vectors that come out of these webs.

Jim Dolan gave a couple of talks while I was there, which actually fit together as two parts of a bigger picture – one was during the workshop itself, and one at the logic seminar on the following Monday. It helped a lot to see both in order to appreciate the overall point, so I’ll mix them a bit indiscriminately. The first was called “Dimensional Analysis is Algebraic Geometry”, and the second “Toposes of Quasicoherent Sheaves on Toric Varieties”. For the purposes of the logic seminar, he gave the slogan of the second talk as “Algebraic Geometry is a branch of Categorical Logic”. Jim’s basic idea was inspired by Bill Lawvere’s concept of a “theory”, which is supposed to extend both “algebraic theories” (such as the “theory of groups”) and theories in the sense of physics.  Any given theory is some structured category, and “models” of the theory are functors into some other category to represent it – it thus has a functor category called its “moduli stack of models”.  A physical theory (essentially, models which depict some contents of the universe) has some parameters.  The “theory of elastic scattering”, for instance, has the masses, and initial and final momenta, of two objects which collide and “scatter” off each other.  The moduli space for this theory amounts to assignments of values to these parameters, which must satisfy some algebraic equations – conservation of energy and momentum (for example, , where ).  So the moduli space is some projective algebraic variety.  Jim explained how “dimensional analysis” in physics is the study of line bundles over such varieties (“dimensions” are just such line bundles, since a “dimension” is a 1-dimensional sort of thing, and “quantities” in those dimensions are sections of the line bundles).  Then there’s a category of such bundles, which are organized into a special sort of symmetric monoidal category – in fact, it’s contrained so much it’s just a graded commutative algebra.

In his second talk, he generalized this to talk about categories of sheaves on some varieties – and, since he was talking in the categorical logic seminar, he proposed a point of view for looking at algebraic geometry in the context of logic.  This view could be summarized as: Every (generalized) space studied by algebraic geometry “is” the moduli space of models for some theory in some doctrine.  The term “doctrine” is Bill Lawvere’s, and specifies what kind of structured category the theory and the target of its models are supposed to be (and of course what kind of functors are allowed as models).  Thus, for instance, toposes (as generalized spaces) are supposed to be thought of as “geometric theories”.  He explained that his “dimensional analysis doctrine” is a special case of this.  As usual when talking to Jim, I came away with the sense that there’s a very large program of ideas lurking behind everything he said, of which only the tip of the iceberg actually made it into the talks.

Next post, when I have time, will talk about the meeting at Erlangen…

 

Quasigroups (Loops), and Relativity

So apparently the “Integral” gamma-ray observatory has put some pretty strong limits on predictions of a “grain size” for spacetime, like in Loop Quantum Gravity, or other theories predicting similar violations of Lorentz invariants which would be detectable in higher- and lower-energy photons coming from distant sources.  (Original paper.)  I didn’t actually hear much about such predictions when I was the conference “Quantum Theory and Gravitation” last month in Zurich, though partly that was because it was focused on bringing together people from a variety of different approaches , so the Loop QG and String Theory camps were smaller than at some other conferences on the same subject.  It was a pretty interesting conference, however (many of the slides and such material can be found here).  As one of the organizers, Jürg Fröhlich, observed in his concluding remarks, it gave grounds for optimism about physics, in that it was clear that we’re nowhere near understanding everything about the universe.  Which seems like a good attitude to have to the situation – and it informs good questions: he asked questions in many of the talks that went right to the heart of the most problematic things about each approach.

Often after attending a conference like that, I’d take the time to do a blog about all the talks – which I was tempted to do, but I’ve been busy with things I missed while I was away, and now it’s been quite a while.  I will probably come back at some point and think about the subject of conformal nets, because there were some interesting talks by Andre Henriques at one workshop I was at, and another by Roberto Longo at this one, which together got me interested in this subject.  But that’s not what I’m going to write about this time.

This time, I want to talk about a different kind of topic.  Talking  in Zurich with various people – John Barrett, John Baez, Laurent Freidel, Derek Wise, and some others, on and off – we kept coming back to kept coming back to various seemingly strange algebraic structures.  One such structure is a “loop“, also known (maybe less confusingly) as a “quasigroup” (in fact, a loop is a quasigroup with a unit).  This was especially confusing, because we were talking about these gadgets in the context of gauge theory, where you might want to think about assigning an element of one as the holonomy around a LOOP in spacetime.  Limitations of the written medium being what they are, I’ll just avoid the problem and say “quasigroup” henceforth, although actually I tend to use “loop” when I’m speaking.

The axioms for a quasigroup look just like the axioms for a group, except that the axiom of associativity is missing.  That is, it’s a set with a “multiplication” operation, and each element has a left and a right inverse, called and .  (I’m also assuming the quasigroup is unital from here on in).  Of course, in a group (which is a special kind of quasigroup where associativity holds), you can use associativity to prove that , but we don’t assume it’s true in a quasigroup.  Of course, you can consider the special case where it IS true: this is a “quasigroup with two-sided inverse”, which is a weaker assumption than associativity.

In fact, this is an example of a kind of question one often asks about quasigroups: what are some extra properties we can suppose which, if they hold for a quasigroup , make life easier?  Associativity is a strong condition to ask, and gives the special case of a group, which is a pretty well-understood area.  So mostly one looks for something weaker than associativity.  Probably the most well-known, among people who know about such things, is the Moufang axiom, named after Ruth Moufang, who did a lot of the pioneering work studying quasigroups.

There are several equivalent ways to state the Moufang axiom, but a nice one is:

Which you could derive from the associative law if you had it, but which doesn’t imply associativity.   With associators, one can go from a fully-right-bracketed to a fully-left-bracketed product of four things: .  There’s no associator here (a quasigroup is a set, not a category – though categorifying this stuff may be a nice thing to try), but the Moufang axiom says this is an equation when .  One might think of the stronger condition that says it’s true for all , but the Moufang axiom turns out to be the more handy one.

One way this is so is found in the division algebras.  A division algebra is a (say, real) vector space with a multiplication for which there’s an identity and a notion of division – that is, an inverse for nonzero elements.  We can generalize this enough that we allow different left and right inverses, but in any case, even if we relax this (and the assumption of associativity), it’s a well-known theorem that there are still only four finite dimensional ones.  Namely, they are , , , and : the real numbers, complex numbers, quaternions, and octonions, with real dimensions 1, 2, 4, and 8 respectively.

So the pattern goes like this.  The first two, and , are commutative and associative.  The quaternions are noncommutative, but still associative.  The octonions are neither commutative nor associative.  They also don’t satisfy that stronger axiom .  However, the octonions do satisfy the Moufang axiom.  In each case, you can get a quasigroup by taking the nonzero elements – or, using the fact that there’s a norm around in the usual way of presenting these algebras, the elements of unit norm.  The unit quaternions, in fact, form a group – specifically, the group .  The unit reals and complexes form abelian groups (respectively, , and ).  These groups all have familiar names.  The quasigroup of unit octonions doesn’t have any other more familiar name.  If you believe in the fundamental importance of this sequence of four division algebras, though, it does suggest that a natural sequence in which to weaken axioms for “multiplication” goes: commutative-and-associative, associative, Moufang.

The Moufang axiom does imply some other commonly suggested weakenings of associativity, as well.  For instance, a quasigroup that satisfies the Moufang axiom must also be alternative (a restricted form of associativity when two copies of one element are next to each other: i.e. the left alternative law , and right alternative law ).

Now, there are various ways one could go with this; the one I’ll pick is toward physics.  The first three entries in that sequence of four division algebras – and the corresponding groups – all show up all over the place in physics.  is the simplest nontrivial group, so this could hardly fail to be true, but at any rate, it appears as, for instance, the symmetry group of the set of orientations on a manifold, or the grading in supersymmetry (hence plays a role distinguishing bosons and fermions), and so on.  is, among any number of other things, the group in which action functionals take their values in Lagrangian quantum mechanics; in the Hamiltonian setup, it’s the group of phases that characterizes how wave functions evolve in time.  Then there’s , which is the (double cover of the) group of rotations of 3-space; as a consequence, its representation theory classifies the “spins”, or angular momenta, that a quantum particle can have.

What about the octonions – or indeed the quasigroup of unit octonions?  This is a little less clear, but I will mention this: John Baez has been interested in octonions for a long time, and in Zurich, gave a talk about what kind of role they might play in physics.  This is supposed to partially explain what’s going on with the “special dimensions” that appear in string theory – these occur where the dimension of a division algebra (and a Clifford algebra that’s associated to it) is the same as the codimension of a string worldsheet.  J.B.’s student, John Huerta, has also been interested in this stuff, and spoke about it here in Lisbon in February – it’s the subject of his thesis, and a couple of papers they’ve written.  The role of the octonions here is not nearly so well understood as elsewhere, and of course whether this stuff is actually physics, or just some interesting math that resembles it, is open to experiment – unlike those other examples, which are definitely physics if anything is!

So at this point, the foregoing sets us up to wonder about two questions.  First: are there any quasigroups that are actually of some intrinsic interest which don’t satisfy the Moufang axiom?  (This might be the next step in that sequence of successively weaker axioms).  Second: are there quasigroups that appear in genuine, experimentally tested physics?  (Supposing you don’t happen to like the example from string theory).

Well, the answer is yes on both counts, with one common example – a non-Moufang quasigroup which is of interest precisely because it has a direct physical interpretation.  This example is the composition of velocities in Special Relativity, and was pointed out to me by Derek Wise as a nice physics-based example of nonassociativity.  That it’s also non-Moufang is also true, and not too surprising once you start trying to check it by a direct calculation: in each case, the reason is that the interpretation of composition is very non-symmetric.  So how does this work?

Well, if we take units where the speed of light is 1, then Special Relativity tells us that relative velocities of two observers are vectors in the interior of .  That is, they’re 3-vectors with length less than 1, since the magnitude of the relative velocity must be less than the speed of light.  In any elementary course on Relativity, you’d learn how to compose these velocities, using the “gamma factor” that describes such things as time-dilation.  This can be derived from first principles, nor is it too complicated, but in any case the end result is a new “addition” for vectors:

where   is the reciprocal of the aforementioned “gamma” factor.  The vectors and are the components of the vector which are parallel to, and perpendicular to, , respectively.

The way this is interpreted is: if is the velocity of observer B as measured by observer A, and is the velocity of observer C as measured by observer B, then is the velocity of observer C as measured by observer A.

Clearly, there’s an asymmetry in how and are treated: the first vector, , is a velocity as seen by the same observer who sees the velocity in the final answer.  The second, , is a velocity as seen by an observer who’s vanished by the time we have in hand.  Just looking at the formular, you can see this is an asymmetric operation that distinguishes the left and right inputs.  So the fact (slightly onerous, but not conceptually hard, to check) that it’s noncommutative, and indeed nonassociative, and even non-Moufang, shouldn’t come as a big shock.

The fact that it makes into a quasigroup is a little less obvious, unless you’ve actually worked through the derivation – but from physical principles, is closed under this operation because the final relative velocity will again be less than the speed of light.  The fact that this has “division” (i.e. cancellation), is again obvious enough from physical principles: if we have , the relative velocity of A and C, and we have one of or – the relative velocity of B to either A or C – then the relative velocity of B to the other one of these two must exist, and be findable using this formula.  That’s the “division” here.

So in fact this non-Moufang quasigroup, exotic-sounding algebraic terminology aside, is one that any undergraduate physics student will have learned about and calculated with.

One point that Derek was making in pointing this example out to me was as a comment on a surprising claim someone (I don’t know who) had made, that mathematical abstractions like “nonassociativity” don’t really appear in physics.  I find the above a pretty convincing case that this isn’t true.

In fact, physics is full of Lie algebras, and the Lie bracket is a nonassociative multiplication (except in trivial cases).  But I guess there is an argument against this: namely, people often think of a Lie algebra as living inside its universal enveloping algebra.  Then the Lie bracket is defined as , using the underlying (associative!) multiplication.  So maybe one can claim that nonassociativity doesn’t “really” appear in physics because you can treat it as a derived concept.

An even simpler example of this sort of phenomenon: the integers with subtraction (rather than addition) are nonassociative, in that .  But this only suggests that subtraction is the wrong operation to use: it was derived from addition, which of course is commutative and associative.

In which case, the addition of velocities in relativity is also a derived concept.  Because, of course, really in SR there are no 3-space “velocities”: there are tangent vectors in Minkowski space, which is a 4-dimensional space.  Adding these vectors in is again, of course, commutative and associative.  The concept of “relative velocity” of two observers travelling along given vectors is a derived concept which gets its strange properties by treating the two arguments asymmetrically, just like like “commutator” and “subtraction” do: you first use one vector to decide on a way of slicing Minkowski spacetime into space and time, and then use this to measure the velocity of the other.

Even the octonions, seemingly the obvious “true” example of nonassociativity, could be brushed aside by someone who really didn’t want to accept any example: they’re constructed from the quaternions by the Cayley-Dickson construction, so you can think of them as pairs of quaternions (or 4-tuples of complex numbers).  Then the nonassociative operation is built from associative ones, via that construction.

So are there any “real” examples of “true” nonassociativity (let alone non-Moufangness) that can’t simply be dismissed as not a fundamental operation by someone sufficiently determined?  Maybe, but none I know of right now.  It may be quite possible to consistently hold that anything nonassociative can’t possibly be fundamental (for that matter, elements of noncommutative groups can be represented by matrices of commuting real numbers).  Maybe it’s just my attitude to fundamentals, but somehow this doesn’t move me much.  Even if there are no “fundamentals” examples, I think those given above suggest a different point: these derived operations have undeniable and genuine meaning – in some cases more immediate than the operations they’re derived from.  Whether or not subtraction, or the relative velocity measured by observers, or the bracket of (say) infinitesimal rotations, are “fundamental” ideas is less important than that they’re practical ones that come up all the time.

 

HGTQGR – Part IIIb (Workshop)

As usual, this write-up process has been taking a while since life does intrude into blogging for some reason.  In this case, because for a little less than a week, my wife and I have been on our honeymoon, which was delayed by our moving to Lisbon.  We went to the Azores, or rather to São Miguel, the largest of the nine islands.  We had a good time, roughly like so:

Now that we’re back, I’ll attempt to wrap up with the summaries of things discussed at the workshop on Higher Gauge Theory, TQFT, and Quantum Gravity.  In the previous post I described talks which I roughly gathered under TQFT and Higher Gauge Theory, but the latter really ramifies out in a few different ways.  As began to be clear before, higher bundles are classified by higher cohomology of manifolds, and so are gerbes – so in fact these are two slightly different ways of talking about the same thing.  I also remarked, in the summary of Konrad Waldorf’s talk, the idea that the theory of gerbes on a manifold is equivalent to ordinary gauge theory on its loop space – which is one way to make explicit the idea that categorification “raises dimension”, in this case from parallel transport of points to that of 1-dimensional loops.  Next we’ll expand on that theme, and then finally reach the “Quantum Gravity” part, and draw the connection between this and higher gauge theory toward the end.

Gerbes and Cohomology

The very first workshop speaker, in fact, was Paolo Aschieri, who has done a lot of work relating noncommutative geometry and gravity.  In this case, though, he was talking about noncommutative gerbes, and specifically referred to this work with some of the other speakers.  To be clear, this isn’t about gerbes with noncommutative group 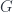, but about gerbes on noncommutative spaces.  To begin with, it’s useful to express gerbes in the usual sense in the right language.  In particular, he explain what a gerbe on a manifold is in concrete terms, giving Hitchin’s definition (viz).  A 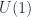gerbe can be described as “a cohomology class” but it’s more concrete to present it as:

• a collection of line bundles associated with double overlaps 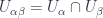.  Note this gets an algebraic structure (multiplication of bundles is pointwise , with an inverse given by the dual, 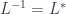, so we can require…
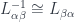• , which helps define…
• transition functions 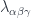on triple overlaps , which are sections of 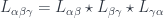.  If this product is trivial, there’d be a 1-cocycle condition here, but we only insist on the 2-cocycle condition…
• 

This is a 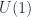-gerbe on a commutative space.  The point is that one can make a similar definition for a noncommutative space.  If the space is associated with the algebra 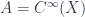of smooth functions, then a line bundle is a module for 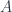, so if 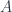is noncommutative (thought of as a “space” ), a “bundle over is just defined to be an 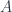-module.  One also has to define an appropriate “covariant derivative” operator 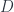on this module, and the -product must be defined as well, and will be noncommutative (we can think of it as a deformation of the above).  The transition functions are sections: that is, elements of the modules in question.  his means we can describe a gerbe in terms of a big stack of modules, with a chosen algebraic structure, together with some elements.  The idea then is that gerbes can give an interpretation of cohomology of noncommutative spaces as well as commutative ones.

Mauro Spera spoke about a point of view of gerbes based on “transgressions”.  The essential point is that an 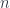-gerbe on a space can be seen as the obstruction to patching together a family of  -gerbes.  Thus, for instance, a 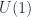0-gerbe is a 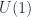-bundle, which is to say a complex line bundle.  As described above, a 1-gerbe can be understood as describing the obstacle to patching together a bunch of line bundles, and the obstacle is the ability to find a cocycle 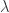satisfying the requisite conditions.  This obstacle is measured by the cohomology of the space.  Saying we want to patch together -gerbes on the fibre.  He went on to discuss how this manifests in terms of obstructions to string structures on manifolds (already discussed at some length in the post on Hisham Sati’s school talk, so I won’t duplicate here).

A talk by Igor Bakovic, “Stacks, Gerbes and Etale Groupoids”, gave a way of looking at gerbes via stacks (see this for instance).  The organizing principle is the classification of bundles by the space maps into a classifying space – or, to get the category of principal 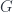-bundles on, the category 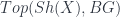, where 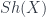is the category of sheaves on and 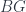is the classifying topos of 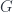-sets.  (So we have geometric morphisms between the toposes as the objects.)  Now, to get further into this, we use that 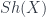is equivalent to the category of Étale spaces over – this is a refinement of the equivalence between bundles and presheaves.  Taking stalks of a presheaf gives a bundle, and taking sections of a bundle gives a presheaf – and these operations are adjoint.

The issue at hand is how to categorify this framework to talk about 2-bundles, and the answer is there’s a 2-adjunction between the 2-category 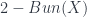of such things, and , the 2-category of fibred categories over .  (That is, instead of looking at “sheaves of sets”, we look at “sheaves of categories” here.)  The adjunction, again, involves talking stalks one way, and taking sections the other way.  One hard part of this is getting a nice definition of “stalk” for stacks (i.e. for the “sheaves of categories”), and a good part of the talk focused on explaining how to get a nice tractable definition which is (fibre-wise) equivalent to the more natural one.

Bakovic did a bunch of this work with Branislav Jurco, who was also there, and spoke about “Nonabelian Bundle 2-Gerbes“.  The paper behind that link has more details, which I’ve yet to entirely absorb, but the essential point appears to be to extend the description of “bundle gerbes” associated to crossed modules up to 2-crossed modules.  Bundles, with a structure-group 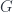, are classified by the cohomology with coefficients in 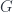; and whereas “bundle-gerbes” with a structure-crossed-module 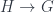can likewise be described by cohomology .  Notice this is a bit different from the description in terms of higher cohomology for a 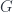-gerbe, which can be understood as a bundle-gerbe using the shifted crossed module 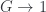(when 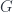is abelian.  The goal here is to generalize this part to nonabelian groups, and also pass up to “bundle 2-gerbes” based on a 2-crossed module, or crossed complex of length 2, 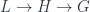as I described previously for Joao Martins’ talk.  This would be classified in terms of cohomology valued in the 2-crossed module.  The point is that one can describe such a thing as a bundle over a fibre product, which (I think – I’m not so clear on this part) deals with the same structure of overlaps as the higher cohomology in the other way of describing things.

Finally,  a talk that’s a little harder to classify than most, but which I’ve put here with things somewhat related to string theory, was Alexander Kahle‘s on “T-Duality and Differential K-Theory”, based on work with Alessandro Valentino.  This uses the idea of the differential refinement of cohomology theories – in this case, K-theory, which is a generalized cohomology theory, which is to say that K-theory satisfies the Eilenberg-Steenrod axioms (with the dimension axiom relaxed, hence “generalized”).  Cohomology theories, including generalized ones, can have differential refinements, which pass from giving topological to geometrical information about a space.  So, while K-theory assigns to a space the Grothendieck ring of the category of vector bundles over it, the differential refinement of K-theory does the same with the category of vector bundles with connection.  This captures both local and global structures, which turns out to be necessary to describe fields in string theory – specifically, Ramond-Ramond fields.  The point of this talk was to describe what happens to these fields under T-duality.  This is a kind of duality in string theory between a theory with large strings and small strings.  The talk describes how this works, where we have a manifold with fibres at each point 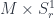with fibres strings of radius and with radius 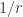.  There’s a correspondence space 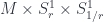, which has projection maps down into the two situations.  Fields, being forms on such a fibration, can be “transferred” through this correspondence space by a “pull-back and push-forward” (with, in the middle, a wedge with a form that mixes the two directions, ).  But to be physically the right kind of field, these “forms” actually need to be representing cohomology classes in the differential refinement of K-theory.

Quantum Gravity etc.

Now, part of the point of this workshop was to try to build, or anyway maintain, some bridges between the kind of work in geometry and topology which I’ve been describing and the world of physics.  There are some particular versions of physical theories where these ideas have come up.  I’ve already touched on string theory along the way (there weren’t many talks about it from a physicist’s point of view), so this will mostly be about a different sort of approach.

Benjamin Bahr gave a talk outlining this approach for our mathematician-heavy audience, with his talk on “Spin Foam Operators” (see also for instance this paper).  The point is that one approach to quantum gravity has a theory whose “kinematics” (the description of the state of a system at a given time) is described by “spin networks” (based on gauge theory), as described back in the pre-school post.  These span a Hilbert space, so the “dynamical” issue of such models is how to get operators between Hilbert spaces from “foams” that interpolate between such networks – that is, what kind of extra data they might need, and how to assign amplitudes to faces and edges etc. to define an operator, which (assuming a “local” theory where distant parts of the foam affect the result independently) will be of the form:

where 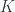is a particular complex (foam), 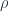is a way of assigning irreps to faces of the foam, and 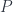is the assignment of intertwiners to edges.  Later on, one can take a discrete version of a path integral by summing over all these 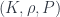.  Here we have a product over faces and one over vertices, with an amplitude 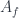assigned (somehow – this is the issue) to faces.  The trace is over all the representation spaces assigned to the edges that are incident to a vertex (this is essentially the only consistent way to assign an amplitude to a vertex).  If we also consider spacetimes with boundary, we need some amplitudes 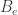at the boundary edges, as well.  A big part of the work with such models is finding such amplitudes that meet some nice conditions.

Some of these conditions are inherently necessary – to ensure the theory is invariant under gauge transformations, or (formally) changing orientations of faces.  Others are considered optional, though to me “functoriality” (that the way of deriving operators respects the gluing-together of foams) seems unavoidable – it imposes that the boundary amplitudes have to be found from the 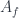in one specific way.  Some other nice conditions might be: that 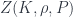depends only on the topology of 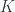(which demands that the 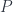operators be projections); that is invariant under subdivision of the foam (which implies the amplitudes have to be ).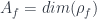

Assuming all these means the only choice is exactly which sub-projection is of the projection onto the gauge-invariant part of the representation space for the faces attached to edge .  The rest of the talk discussed this, including some examples (models for BF-theory, the Barrett-Crane model and the more recent EPRL/FK model), and finished up by discussing issues about getting a nice continuum limit by way of “coarse graining”.

On a related subject, Bianca Dittrich spoke about “Dynamics and Diffeomorphism Symmetry in Discrete Quantum Gravity”, which explained the nature of some of the hard problems with this sort of discrete model of quantum gravity.  She began by asking what sort of models (i.e. which choices of amplitudes) in such discrete models would actually produce a nice continuum theory – since gravity, classically, is described in terms of spacetimes which are continua, and the quantum theory must look like this in some approximation.  The point is to think of these as “coarse-graining” of a very fine (perfect, in the limit) approximation to the continuum by a triangulation with a very short length-scale for the edges.  Coarse graining means discarding some of the edges to get a coarser approximation (perhaps repeatedly).  If the happens to be triangulation-independent, then coarse graining makes no difference to the result, nor does the converse process of refining the triangulation.  So one question is:  if we expect the continuum limit to be diffeomorphism invariant (as is General Relativity), what does this say at the discrete level?  The relation between diffeomorphism invariance and triangulation invariance has been described by Hendryk Pfeiffer, and in the reverse direction by Dittrich et al.

Actually constructing the dynamics for a system like this in a nice way (“canonical dynamics with anomaly-free constraints”) is still a big problem, which Bianca suggested might be approached by this coarse-graining idea.  Now, if a theory is topological (here we get the link to TQFT), such as electromagnetism in 2D, or (linearized) gravity in 3D, coarse graining doesn’t change much.  But otherwise, changing the length scale means changing the action for the continuum limit of the theory.  This is related to renormalization: one starts with a “naive” guess at a theory, then refines it (in this case, by the coarse-graining process), which changes the action for the theory, until arriving at (or approximating to) a fixed point.  Bianca showed an example, which produces a really huge, horrible action full of very complicated terms, which seems rather dissatisfying.  What’s more, she pointed out that, unless the theory is topological, this always produces an action which is non-local – unlike the “naive” discrete theory.  That is, the action can’t be described in terms of a bunch of non-interacting contributions from the field at individual points – instead, it’s some function which couples the field values at distant points (albeit in a way that falls off exponentially as the points get further apart).

In a more specific talk, Aleksandr Mikovic discussed “Finiteness and Semiclassical Limit of EPRL-FK Spin Foam Models”, looking at a particular example of such models which is the (relatively) new-and-improved candidate for quantum gravity mentioned above.  This was a somewhat technical talk, which I didn’t entirely follow, but  roughly, the way he went at this was through the techniques of perturbative QFT.  That is, by looking at the theory in terms of an “effective action”, instead of some path integral over histories with action – which looks like .  Starting with some classical history – a stationary point of the action – the effective action is an integral over small fluctuations 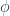around it of .

He commented more on the distinction between the question of triangulation independence (which is crucial for using spin foams to give invariants of manifolds) and the question of whether the theory gives a good quantum theory of gravity – that’s the “semiclassical limit” part.  (In light of the above, this seems to amount to asking if “diffeomorphism invariance” really extends through to the full theory, or is only approximately true, in the limiting case).  Then the “finiteness” part has to do with the question of getting decent asymptotic behaviour for some of those weights mentioned above so as to give a nice effective action (if not necessarily triangulation independence).  So, for instance, in the Ponzano-Regge model (which gives a nice invariant for manifolds), the vertex amplitudes are found by the 6j-symbols of representations.  The asymptotics of the 6j symbols then becomes an issue – Alekandr noted that to get a theory with a nice effective action, those 6j-symbols need to be scaled by a certain factor.  This breaks triangulation independence (hence means we don’t have a good manifold invariant), but gives a physically nicer theory.  In the case of 3D gravity, this is not what we want, but as he said, there isn’t a good a-priori reason to think it can’t give a good theory of 4D gravity.

Now, making a connection between these sorts of models and higher gauge theory, Aristide Baratin spoke about “2-Group Representations for State Sum Models”.  This is a project Baez, Freidel, and Wise, building on work by Crane and Sheppard (see my previous post, where Derek described the geometry of the representation theory for some 2-groups).  The idea is to construct state-sum models where, at the kinematical level, edges are labelled by 2-group representations, faces by intertwiners, and tetrahedra by 2-intertwiners.  (This assumes the foam is a triangulation – there’s a certain amount of back-and-forth in this area between this, and the Poincaré dual picture where we have 4-valent vertices).  He discussed this in a couple of related cases – the Euclidean and Poincaré 2-groups, which are described by crossed modules with base groups or respectively, acting on the abelian group (of automorphisms of the identity) in the obvious way.  Then the analogy of the 6j symbols above, which are assigned to tetrahedra (or dually, vertices in a foam interpolating two kinematical states), are now 10j symbols assigned to 4-simplexes (or dually, vertices in the foam).

One nice thing about this setup is that there’s a good geometric interpretation of the kinematics – irreducible representations of these 2-groups pick out orbits of the action of the relevant 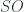on .  These are “mass shells” – radii of spheres in the Euclidean case, or proper length/time values that pick out hyperboloids in the Lorentzian case of .  Assigning these to edges has an obvious geometric meaning (as a proper length of the edge), which thus has a continuous spectrum.  The areas and volumes interpreting the intertwiners and 2-intertwiners start to exhibit more of the discreteness you see in the usual formulation with representations of the 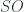groups themselves.  Finally, Aristide pointed out that this model originally arose not from an attempt to make a quantum gravity model, but from looking at Feynman diagrams in flat space (a sort of “quantum flat space” model), which is suggestively interesting, if not really conclusively proving anything.

Finally, Laurent Freidel gave a talk, “Classical Geometry of Spin Network States” which was a way of challenging the idea that these states are exclusively about “quantum geometries”, and tried to give an account of how to interpret them as discrete, but classical.  That is, the quantization of the classical phase space (the cotangent bundle of connections-mod-gauge) involves first a discretization to a spin-network phase space , and then a quantization to get a Hilbert space , and the hard part is the first step.  The point is to see what the classical phase space is, and he describes it as a (symplectic) quotient , which starts by assigning $T^*(SU(2))$ to each edge, then reduced by gauge transformations.  The puzzle is to interpret the states as geometries with some discrete aspect.

The answer is that one thinks of edges as describing (dual) faces, and vertices as describing some polytopes.  For each , there’s a -dimensional “shape space” of convex polytopes with -faces and a given fixed area 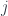.  This has a canonical symplectic structure, where lengths and interior angles at an edge are the canonically conjugate variables.  Then the whole phase space describes ways of building geometries by gluing these things (associated to vertices) together at the corresponding faces whenever the two vertices are joined by an edge.  Notice this is a bit strange, since there’s no particular reason the faces being glued will have the same shape: just the same area.  An area-1 pentagon and an area-1 square associated to the same edge could be glued just fine.  Then the classical geometry for one of these configurations is build of a bunch of flat polyhedra (i.e. with a flat metric and connection on them).  Measuring distance across a face in this geometry is a little strange.  Given two points inside adjacent cells, you measure orthogonal distance to the matched faces, and add in the distance between the points you arrive at (orthogonally) – assuming you glued the faces at the centre.  This is a rather ugly-seeming geometry, but it’s symplectically isomorphic to the phase space of spin network states – so it’s these classical geometries that spin-foam QG is a quantization of.  Maybe the ugliness should count against this model of quantum gravity – or maybe my aesthetic sense just needs work.

(Laurent also gave another talk, which was originally scheduled as one of the school talks, but ended up being a very interesting exposition of the principle of “Relativity of Localization”, which is hard to shoehorn into the themes I’ve used here, and was anyway interesting enough that I’ll devote a separate post to it.)

 

HGTQGR – Part IIIa (Workshop)

Now for a more sketchy bunch of summaries of some talks presented at the HGTQGR workshop.  I’ll organize this into a few themes which appeared repeatedly and which roughly line up with the topics in the title: in this post, variations on TQFT, plus 2-group and higher forms of gauge theory; in the next post, gerbes and cohomology, plus talks on discrete models of quantum gravity and suchlike physics.

TQFT and Variations

I start here for no better reason than the personal one that it lets me put my talk first, so I’m on familiar ground to start with, for which reason also I’ll probably give more details here than later on.  So: a TQFT is a linear representation of the category of cobordisms – that is, a (symmetric monoidal) functor , in the notation I mentioned in the first school post.  An Extended TQFT is a higher functor , representing a category of cobordisms with corners into a higher category of k-Vector spaces (for some definition of same).  The essential point of my talk is that there’s a universal construction that can be used to build one of these at , which relies on some way of representing into , whose objects are groupoids, and whose morphisms in are pairs of groupoid homomorphisms .  The 2-morphisms have an analogous structure.  The point is that there’s a 2-functor which is takes representations of groupoids, at the level of objects; for morphisms, there is a “pull-push” operation that just uses the restricted and induced representation functors to move a representation across a span; the non-trivial (but still universal) bit is the 2-morphism map, which uses the fact that the restriction and induction functors are bi-ajdoint, so there are units and counits to use.  A construction using gauge theory gives groupoids of connections and gauge transformations for each manifold or cobordism.  This recovers a form of the Dijkgraaf-Witten model.  In principle, though, any way of getting a groupoid (really, a stack) associated to a space functorially will give an ETQFT this way.  I finished up by suggesting what would need to be done to extend this up to higher codimension.  To go to codimension 3, one would assign an object (codimension-3 manifold) a 3-vector space which is a representation 2-category of 2-groupoids of connections valued in 2-groups, and so on.  There are some theorems about representations of n-groupoids which would need to be proved to make this work.

The fact that different constructions can give groupoids for spaces was used by the next speaker, Thomas Nicklaus, whose talk described another construction that uses the I mentioned above.  This one produces “Equivariant Dijkgraaf-Witten Theory”.  The point is that one gets groupoids for spaces in a new way.  Before, we had, for a space a groupoid whose objects are -connections (or, put another way, bundles-with-connection) and whose morphisms are gauge transformations.  Now we suppose that there’s some group which acts weakly (i.e. an action defined up to isomorphism) on .  We think of this as describing “twisted bundles” over .  This is described by a quotient stack (which, as a groupoid, gets some extra isomorphisms showing where two objects are related by the -action).  So this gives a new map , and applying gives a TQFT.  The generating objects for the resulting 2-vector space are “twisted sectors” of the equivariant DW model.  There was some more to the talk, including a description of how the DW model can be further mutated using a cocycle in the group cohomology of , but I’ll let you look at the slides for that.

Next up was Jamie Vicary, who was talking about “(1,2,3)-TQFT”, which is another term for what I called “Extended” TQFT above, but specifying that the objects are 1-manifolds, the morphisms 2-manifolds, and the 2-morphisms are 3-manifolds.  He was talking about a theorem that identifies oriented TQFT’s of this sort with “anomaly-free modular tensor categories” – which is widely believed, but in fact harder than commonly thought.  It’s easy enough that such a TQFT corresponds to a MTC – it’s the category assigned to the circle.  What’s harder is showing that the TQFT’s are equivalent functors iff the categories are equivalent.  This boils down, historically, to the difficulty of showing the category is rigid.  Jamie was talking about a project with Bruce Bartlett and Chris Schommer-Pries, whose presentation of the cobordism category (described in the school post) was the basis of their proof.

Part of it amounts to giving a description of the TQFT in terms of certain string diagrams.  Jamie kindly credited me with describing this point of view to him: that the codimension-2 manifolds in a TQFT can be thought of as “boundaries in space” – codimension-1 manifolds are either time-evolving boundaries, or else slices of space in which the boundaries live; top-dimension cobordisms are then time-evolving slices of space-with-boundary.  (This should be only a heuristic way of thinking – certainly a generic TQFT has no literal notion of “time-evolution”, though in that (2+1) quantum gravity can be seen as a TQFT, there’s at least one case where this picture could be taken literally.)  Then part of their proof involves showing that the cobordisms can be characterized by taking vector spaces on the source and target manifolds spanned by the generating objects, and finding the functors assigned to cobordisms in terms of sums over all “string diagrams” (particle worldlines, if you like) bounded by the evolving boundaries.  Jamie described this as a “topological path integral”.  Then one has to describe the string diagram calculus – ridigidy follows from the “yanking” rule, for instance, and this follows from Morse theory as in Chris’ presentation of the cobordism category.

There was a little more discussion about what the various properties (proved in a similar way) imply.  One is “cloaking” – the fact that a 2-morphism which “creates a handle” is invisible to the string diagrams in the sense that it introduces a sum over all diagrams with a string “looped” around the new handle, but this sum gives a result that’s equal to the original map (in any “pivotal” tensor category, as here).

Chronologically before all these, one of the first talks on such a topic was by Rafael Diaz, on Homological Quantum Field Theory, or HLQFT for short, which is a rather different sort of construction.  Remember that Homotopy QFT, as described in my summary of Tim Porter’s school sessions, is about linear representations of what I’ll for now call , whose morphisms are -dimensional cobordisms equipped with maps into a space up to homotopy.  HLQFT instead considers cobordisms equipped with maps taken up to homology.

Specifically, there’s some space , say a manifold, with some distinguished submanifolds (possibly boundary components; possibly just embedded submanifolds; possibly even all of for a degenerate case).  Then we define to have objects which are -manifolds equipped with maps into which land on the distinguished submanifolds (to make composition work nicely, we in fact assume they map to a single point).  Morphisms in are trickier, and look like : a cobordism in this category is likewise equipped with a map from its boundary into which recovers the maps on its objects.  That is a homology class of maps from to , which agrees with .  This forms a monoidal category as with standard cobordisms.  Then HLQFT is about representations of this category.  One simple case Rafael described is the dimension-1 case, where objects are (ordered sets of) points equipped with maps that pick out chosen submanifolds of , and morphisms are just braids equipped with homology classes of “paths” joining up the source and target submanifolds.  Then a representation might, e.g., describe how to evolve a homology class on the starting manifold to one on the target by transporting along such a path-up-to-homology.  In higher dimensions, the evolution is naturally more complicated.

A slightly looser fit to this section is the talk by Thomas Krajewski, “Quasi-Quantum Groups from Strings” (see this) – he was talking about how certain algebraic structures arise from “string worldsheets”, which are another way to describe cobordisms.  This does somewhat resemble the way an algebraic structure (Frobenius algebra) is related to a 2D TQFT, but here the string worldsheets are interacting with 3-form field, (the curvature of that 2-form field of string theory) and things needn’t be topological, so the result is somewhat different.

Part of the point is that quantizing such a thing gives a higher version of what happens for quantizing a moving particle in a gauge field.  In the particle case, one comes up with a line bundle (of which sections form the Hilbert space) and in the string case one comes up with a gerbe; for the particle, this involves associated 2-cocycle, and for the string a 3-cocycle; for the particle, one ends up producing a twisted group algebra, and for the string, this is where one gets a “quasi-quantum group”.  The algebraic structures, as in the TQFT situation, come from, for instance, the “pants” cobordism which gives a multiplication and a comultiplication (by giving maps or the reverse, where is the object assigned to a circle).

There is some machinery along the way which I won’t describe in detail, except that it involves a tricomplex of forms – the gradings being form degree, the degree of a cocycle for group cohomology, and the number of overlaps.  As observed before, gerbes and their higher versions have transition functions on higher numbers of overlapping local neighborhoods than mere bundles.  (See the paper above for more)

Higher Gauge Theory

The talks I’ll summarize here touch on various aspects of higher-categorical connections or 2-groups (though at least one I’ll put off until later).  The division between this and the section on gerbes is a little arbitrary, since of course they’re deeply connected, but I’m making some judgements about emphasis or P.O.V. here.

Apart from giving lectures in the school sessions, John Huerta also spoke on “Higher Supergroups for String Theory”, which brings “super” (i.e. -graded) objects into higher gauge theory.  There are “super” versions of vector spaces and manifolds, which decompose into “even” and “odd” graded parts (a.k.a. “bosonic” and “fermionic” parts).  Thus there are “super” variants of Lie algebras and Lie groups, which are like the usual versions, except commutation properties have to take signs into account (e.g. a Lie superalgebra’s bracket is commutative if the product of the grades of two vectors is odd, anticommutative if it’s even).  Then there are Lie 2-algebras and 2-groups as well – categories internal to this setting.  The initial question has to do with whether one can integrate some Lie 2-algebra structures to Lie 2-group structures on a spacetime, which depends on the existence of some globally smooth cocycles.  The point is that when spacetime is of certain special dimensions, this can work, namely dimensions 3, 4, 6, and 10.  These are all 2 more than the real dimensions of the four real division algebras, , , and .  It’s in these dimensions that Lie 2-superalgebras can be integrated to Lie 2-supergroups.  The essential reason is that a certain cocycle condition will hold because of the properties of a form on the Clifford algebras that are associated to the division algebras.  (John has some related material here and here, though not about the 2-group case.)

Since we’re talking about higher versions of Lie groups/algebras, an important bunch of concepts to categorify are those in representation theory.  Derek Wise spoke on “2-Group Representations and Geometry”, based on work with Baez, Baratin and Freidel, most fully developed here, but summarized here.  The point is to describe the representation theory of Lie 2-groups, in particular geometrically.  They’re to be represented on (in general, infinite-dimensional) 2-vector spaces of some sort, which is chosen to be a category of measurable fields of Hilbert spaces on some measure space, which is called (intended to resemble, but not exactly be the same as, , the space of “functors into from the space , the way Kapranov-Voevodsky 2-vector spaces can be described as ).  The first work on this was by Crane and Sheppeard, and also Yetter.  One point is that for 2-groups, we have not only representations and intertwiners between them, but 2-intertwiners between these.  One can describe these geometrically – part of which is a choice of that measure space .

This done, we can say that a representation of a 2-group is a 2-functor , where is seen as a one-object 2-category.  Thinking about this geometrically, if we concretely describe by the crossed module , defines an action of on , and a map into the character group, which thereby becomes a -equivariant bundle.  One consequence of this description is that it becomes possible to distinguish not only irreducible representations (bundles over a single orbit) and indecomposible ones (where the fibres are particularly simple homogeneous spaces), but an intermediate notion called “irretractible” (though it’s not clear how much this provides).  An intertwining operator between reps over and can be described in terms of a bundle of Hilbert spaces – which is itself defined over the pullback of and seen as -bundles over .  A 2-intertwiner is a fibre-wise map between two such things.  This geometric picture specializes in various ways for particular examples of 2-groups.  A physically interesting one, which Crane and Sheppeard, and expanded on in that paper of [BBFW] up above, deals with the Poincaré 2-group, and where irreducible representations live over mass-shells in Minkowski space (or rather, the dual of ).

Moving on from 2-group stuff, there were a few talks related to 3-groups and 3-groupoids.  There are some new complexities that enter here, because while (weak) 2-categories are all (bi)equivalent to strict 2-categories (where things like associativity and the interchange law for composing 2-cells hold exactly), this isn’t true for 3-categories.  The best strictification result is that any 3-category is (tri)equivalent to a Gray category – where all those properties hold exactly, except for the interchange law for horizontal and vertical compositions of 2-cells, which is replaced by an “interchanger” isomorphism with some coherence properties.  John Barrett gave an introduction to this idea and spoke about “Diagrams for Gray Categories”, describing how to represent morphisms, 2-morphisms, and 3-morphisms in terms of higher versions of “string” diagrams involving (piecewise linear) surfaces satisfying some properties.  He also carefully explained how to reduce the dimensions in order to make them both clearer and easier to draw.  Bjorn Gohla spoke on “Mapping Spaces for Gray Categories”, but since it was essentially a shorter version of a talk I’ve already posted about, I’ll leave that for now, except to point out that it linked to the talk by Joao Faria Martins, “3D Holonomy” (though see also this paper with Roger Picken).

The point in Joao’s talk starts with the fact that we can describe holonomies for 3-connections on 3-bundles valued in Gray-groups (i.e. the maximally strict form of a general 3-group) in terms of Gray-functors .  Here, is the fundamental 3-groupoid of , which turns points, paths, homotopies of paths, and homotopies of homotopies into a Gray groupoid (modulo some technicalities about “thin” or “laminated”  homotopies) and is a gauge Gray-group.  Just as a 2-group can be represented by a crossed module, a Gray (3-)group can be represented by a “2-crossed module” (yes, the level shift in the terminology is occasionally confusing).  This is a chain of groups , where acts on the other groups, together with some structure maps (for instance, the Peiffer commutator for a crossed module becomes a lifting ) which all fit together nicely.  Then a tri-connection can be given locally by forms valued in the Lie algebras of these groups: in  .  Relating the global description in terms of and local description in terms of is a matter of integrating forms over paths, surfaces, or 3-volumes that give the various -morphisms of .  This sort of construction of parallel transport as functor has been developed in detail by Waldorf and Schreiber (viz. these slides, or the full paper), some time ago, which is why, thematically, they’re the next two speakers I’ll summarize.

Konrad Waldorf spoke about “Abelian Gauge Theories on Loop Spaces and their Regression”.  (For more, see two papers by Konrad on this)  The point here is that there is a relation between two kinds of theories – string theory (with -field) on a manifold , and ordinary gauge theory on its loop space .  The relation between them goes by the name “regression” (passing from gauge theory on to string theory on ), or “transgression”, going the other way.  This amounts to showing an equivalence of categories between [principal -bundles with connection on ] and [-gerbes with connection on ].  This nicely gives a way of seeing how gerbes “categorify” bundles, since passing to the loop space – whose points are maps means a holonomy functor is now looking at objects (points in ) which would be morphisms in the fundamental groupoid of , and morphisms which are paths of loops (surfaces in which trace out homotopies).  So things are shifted by one level.  Anyway, Konrad explained how this works in more detail, and how it should be interpreted as relating connections on loop space to the -field in string theory.

Urs Schreiber kicked the whole categorification program up a notch by talking about -Connections and their Chern-Simons Functionals .  So now we’re getting up into -categories, and particularly -toposes (see Jacob Lurie’s paper, or even book if so inclined to find out what these are), and in particular a “cohesive topos”, where derived geometry can be developed (Urs suggested people look here, where a bunch of background is collected). The point is that -topoi are good for talking about homotopy theory.  We want a setting which allows all that structure, but also allows us to do differential geometry and derived geometry.  So there’s a “cohesive” -topos called , of “sheaves” (in the -topos sense) of -groupoids on smooth manifolds.  This setting is the minimal common generalization of homotopy theory and differential geometry.

This is about a higher analog of this setup: since there’s a smooth classifying space (in fact, a Lie groupoid) for -bundles, , there’s also an equivalence between categories of -principal bundles, and (of functors into ).  Moreover, there’s a similar setup with for bundles with connection.  This can be described topologically, or there’s also a “differential refinement” to talk about the smooth situation.  This equivalence lives within a category of (smooth) sheaves of groupoids.  For higher gauge theory, we want a higher version as in described above.  Then we should get an equivalence – in this cohesive topos – of and a category of –-gerbes.

Then the part about the  “Chern-Simons functionals” refers to the fact that CS theory for a manifold (which is a kind of TQFT) is built using an action functional that is found as an integral of the forms that describe some -connection over the manifold.  (Then one does a path-integral of this functional over all connections to find partition functions etc.)  So the idea is that for these higher -gerbes, whose classifying spaces we’ve just described, there should be corresponding functionals.  This is why, as Urs remarked in wrapping up, this whole picture has an explicit presentation in terms of forms.  Actually, in terms of Cech-cocycles (due to the fact we’re talking about gerbes), whose coefficients are taken in sheaves of complexes (this is the derived geometry part) of differential forms whose coefficients are in -algebroids (the -groupoid version of Lie algebras, since in general we’re talking about a theory with gauge -groupoids now).

Whew!  Okay, that’s enough for this post.  Next time, wrapping up blogging the workshop, finally.