One talk at the workshop was nominally a school talk by Laurent Freidel, but it’s interesting and distinctive enough in its own right that I wanted to consider it by itself. It was based on this paper on the “Principle of Relative Locality”. This isn’t so much a new theory, as an exposition of what ought to happen when one looks at a particular limit of any putative theory that has both quantum field theory and gravity as (different) limits of it. This leads through some ideas, such as curved momentum space, which have been kicking around for a while. The end result is a way of accounting for apparently non-local interactions of particles, by saying that while the particles themselves “see” the interactions as local, distant observers might not.
Whereas Einstein’s gravity describes a regime where Newton’s gravitational constant is important but Planck’s constant
is negligible, and (special-relativistic) quantum field theory assumes
significant but
not. Both of these assume there is a special velocity scale, given by the speed of light
, whereas classical mechanics assumes that all three can be neglected (i.e.
and
are zero, and
is infinite). The guiding assumption is that these are all approximations to some more fundamental theory, called “quantum gravity” just because it accepts that both
and
(as well as
) are significant in calculating physical effects. So GR and QFT incorporate two of the three constants each, and classical mechanics incorporates neither. The “principle of relative locality” arises when we consider a slightly different approximation to this underlying theory.
This approximation works with a regime where and
are each negligible, but the ratio is not – this being related to the Planck mass
. The point is that this is an approximation with no special length scale (“Planck length”), but instead a special energy scale (“Planck mass”) which has to be preserved. Since energy and momentum are different parts of a single 4-vector, this is also a momentum scale; we expect to see some kind of deformation of momentum space, at least for momenta that are bigger than this scale. The existence of this scale turns out to mean that momenta don’t add linearly – at least, not unless they’re very small compared to the Planck scale.
So what is “Relative Locality”? In the paper linked above, it’s stated like so:
Physics takes place in phase space and there is no invariant global projection that gives a description of processes in spacetime. From their measurements local observers can construct descriptions of particles moving and interacting in a spacetime, but different observers construct different spacetimes, which are observer-dependent slices of phase space.
Motivation
This arises from taking the basic insight of general relativity – the requirement that physical principles should be invariant under coordinate transformations (i.e. diffeomorphisms) – and extend it so that instead of applying just to spacetime, it applies to the whole of phase space. Phase space (which, in this limit where , replaces the Hilbert space of a truly quantum theory) is the space of position-momentum configurations (of things small enough to treat as point-like, in a given fixed approximation). Having no
means we don’t need to worry about any dynamical curvature of “spacetime” (which doesn’t exist), and having no Planck length means we can blithely treat phase space as a manifold with coordinates valued in the real line (which has no special scale). Yet, having a special mass/momentum scale says we should see some purely combined “quantum gravity” effects show up.
The physical idea is that phase space is an accurate description of what we can see and measure locally. Observers (whom we assume small enough to be considered point-like) can measure their own proper time (they “have a clock”) and can detect momenta (by letting things collide with them and measuring the energy transferred locally and its direction). That is, we “see colors and angles” (i.e. photon energies and differences of direction). Beyond this, one shouldn’t impose any particular theory of what momenta do: we can observe the momenta of separate objects and see what results when they interact and deduce rules from that. As an extension of standard physics, this model is pretty conservative. Now, conventionally, phase space would be the cotangent bundle of spacetime . This model is based on the assumption that objects can be at any point, and wherever they are, their space of possible momenta is a vector space. Being a bundle, with a global projection onto
(taking
to
), is exactly what this principle says doesn’t necessarily obtain. We still assume that phase space will be some symplectic manifold. But we don’t assume a priori that momentum coordinates give a projection whose fibres happen to be vector spaces, as in a cotangent bundle.
Now, a symplectic manifold still looks locally like a cotangent bundle (Darboux’s theorem). So even if there is no universal “spacetime”, each observer can still locally construct a version of “spacetime” by slicing up phase space into position and momentum coordinates. One can, by brute force, extend the spacetime coordinates quite far, to distant points in phase space. This is roughly analogous to how, in special relativity, each observer can put their own coordinates on spacetime and arrive at different notions of simultaneity. In general relativity, there are issues with trying to extend this concept globally, but it can be done under some conditions, giving the idea of “space-like slices” of spacetime. In the same way, we can construct “spacetime-like slices” of phase space.
Geometrizing Algebra
Now, if phase space is a cotangent bundle, momenta can be added (the fibres of the bundle are vector spaces). Some more recent ideas about “quasi-Hamiltonian spaces” (initially introduced by Alekseev, Malkin and Meinrenken) conceive of momenta as “group-valued” – rather than taking values in the dual of some Lie algebra (the way, classically, momenta are dual to velocities, which live in the Lie algebra of infinitesimal translations). For small momenta, these are hard to distinguish, so even group-valued momenta might look linear, but the premise is that we ought to discover this by experiment, not assumption. We certainly can detect “zero momentum” and for physical reasons can say that given two things with two momenta , there’s a way of combining them into a combined momentum
. Think of doing this physically – transfer all momentum from one particle to another, as seen by a given observer. Since the same momentum at the observer’s position can be either coming in or going out, this operation has a “negative” with
.
We do have a space of momenta at any given observer’s location – the total of all momenta that can be observed there, and this space now has some algebraic structure. But we have no reason to assume up front that is either commutative or associative (let alone that it makes momentum space at a given observer’s location into a vector space). One can interpret this algebraic structure as giving some geometry. The commutator for
gives a metric on momentum space. This is a bilinear form which is implicitly defined by the “norm” that assigns a kinetic energy to a particle with a given momentum. The associator given by
, infinitesimally near
where this makes sense, gives a connection. This defines a “parallel transport” of a finite momentum
in the direction of a momentum
by saying infinitesimally what happens when adding
to
.
Various additional physical assumptions – like the momentum-space “duals” of the equivalence principle (that the combination of momenta works the same way for all kinds of matter regardless of charge), or the strong equivalence principle (that inertial mass and rest mass energy per the relation are the same) and so forth can narrow down the geometry of this metric and connection. Typically we’ll find that it needs to be Lorentzian. With strong enough symmetry assumptions, it must be flat, so that momentum space is a vector space after all – but even with fairly strong assumptions, as with general relativity, there’s still room for this “empty space” to have some intrinsic curvature, in the form of a momentum-space “dual cosmological constant”, which can be positive (so momentum space is closed like a sphere), zero (the vector space case we usually assume) or negative (so momentum space is hyperbolic).
This geometrization of what had been algebraic is somewhat analogous to what happened with velocities (i.e. vectors in spacetime)) when the theory of special relativity came along. Insisting that the “invariant” scale be the same in every reference system meant that the addition of velocities ceased to be linear. At least, it did if you assume that adding velocities has an interpretation along the lines of: “first, from rest, add velocity v to your motion; then, from that reference frame, add velocity w”. While adding spacetime vectors still worked the same way, one had to rephrase this rule if we think of adding velocities as observed within a given reference frame – this became
(scaling so
and assuming the velocities are in the same direction). When velocities are small relative to
, this looks roughly like linear addition. Geometrizing the algebra of momentum space is thought of a little differently, but similar things can be said: we think operationally in terms of combining momenta by some process. First transfer (group-valued) momentum
to a particle, then momentum
– the connection on momentum space tells us how to translate these momenta into the “reference frame” of a new observer with momentum shifted relative to the starting point. Here again, the special momentum scale
(which is also a mass scale since a momentum has a corresponding kinetic energy) is a “deformation” parameter – for momenta that are small compared to this scale, things seem to work linearly as usual.
There’s some discussion in the paper which relates this to DSR (either “doubly” or “deformed” special relativity), which is another postulated limit of quantum gravity, a variation of SR with both a special velocity and a special mass/momentum scale, to consider “what SR looks like near the Planck scale”, which treats spacetime as a noncommutative space, and generalizes the Lorentz group to a Hopf algebra which is a deformation of it. In DSR, the noncommutativity of “position space” is directly related to curvature of momentum space. In the “relative locality” view, we accept a classical phase space, but not a classical spacetime within it.
Physical Implications
We should understand this scale as telling us where “quantum gravity effects” should start to become visible in particle interactions. This is a fairly large scale for subatomic particles. The Planck mass as usually given is about 21 micrograms: small for normal purposes, about the size of a small sand grain, but very large for subatomic particles. Converting to momentum units with , this is about 6 kg m/s: on the order of the momentum of a kicked soccer ball or so. For a subatomic particle this is a lot.
This scale does raise a question for many people who first hear this argument, though – that quantum gravity effects should become apparent around the Planck mass/momentum scale, since macro-objects like the aforementioned soccer ball still seem to have linearly-additive momenta. Laurent explained the problem with this intuition. For interactions of big, extended, but composite objects like soccer balls, one has to calculate not just one interaction, but all the various interactions of their parts, so the “effective” mass scale where the deformation would be seen becomes where
is the number of particles in the soccer ball. Roughly, the point is that a soccer ball is not a large “thing” for these purposes, but a large conglomeration of small “things”, whose interactions are “fundamental”. The “effective” mass scale tells us how we would have to alter the physical constants to be able to treat it as a “thing”. (This is somewhat related to the question of “effective actions” and renormalization, though these are a bit more complicated.)
There are a number of possible experiments suggested in the paper, which Laurent mentioned in the talk. One involves a kind of “twin paradox” taking place in momentum space. In “spacetime”, a spaceship travelling a large loop at high velocity will arrive where it started having experienced less time than an observer who remained there (because of the Lorentzian metric) – and a dual phenomenon in momentum space says that particles travelling through loops (also in momentum space) should arrive displaced in space because of the relativity of localization. This could be observed in particle accelerators where particles make several transits of a loop, since the effect is cumulative. Another effect could be seen in astronomical observations: if an observer is observing some distant object via photons of different wavelengths (hence momenta), she might “localize” the object differently – that is, the two photons travel at “the same speed” the whole way, but arrive at different times because the observer will interpret the object as being at two different distances for the two photons.
This last one is rather weird, and I had to ask how one would distinguish this effect from a variable speed of light (predicted by certain other ideas about quantum gravity). How to distinguish such effects seems to be not quite worked out yet, but at least this is an indication that there are new, experimentally detectible, effects predicted by this “relative locality” principle. As Laurent emphasized, once we’ve noticed that not accepting this principle means making an a priori assumption about the geometry of momentum space (even if only in some particular approximation, or limit, of a true theory of quantum gravity), we’re pretty much obliged to stop making that assumption and do the experiments. Finding our assumptions were right would simply be revealing which momentum space geometry actually obtains in the approximation we’re studying.
A final note about the physical interpretation: this “relative locality” principle can be discovered by looking (in the relevant limit) at a Lagrangian for free particles, with interactions described in terms of momenta. It so happens that one can describe this without referencing a “real” spacetime: the part of the action that allows particles to interact when “close” only needs coordinate functions, which can certainly exist here, but are an observer-dependent construct. The conservation of (non-linear) momenta is specified via a Lagrange multiplier. The whole Lagrangian formalism for the mechanics of colliding particles works without reference to spacetime. Now, even though all the interactions (specified by the conservation of momentum terms) happen “at one location”, in that there will be an observer who sees them happening in the momentum space of her own location. But an observer at a different point may disagree about whether the interaction was local – i.e. happened at a single point in spacetime. Thus “relativity of localization”.
Again, this is no more bizarre (mathematically) than the fact that distant, relatively moving, observers in special relativity might disagree about simultaneity, whether two events happened at the same time. They have their own coordinates on spacetime, and transferring between them mixes space coordinates and time coordinates, so they’ll disagree whether the time-coordinate values of two events are the same. Similarly, in this phase-space picture, two different observers each have a coordinate system for splitting phase space into “spacetime” and “energy-momentum” coordinates, but switching between them may mix these two pieces. Thus, the two observers will disagree about whether the spacetime-coordinate values for the different interacting particles are the same. And so, one observer says the interaction is “local in spacetime”, and the other says it’s not. The point is that it’s local for the particles themselves (thinking of them as observers). All that’s going on here is the not-very-astonishing fact that in the conventional picture, we have no problem with interactions being nonlocal in momentum space (particles with very different momenta can interact as long as they collide with each other)… combined with the inability to globally and invariantly distinguish position and momentum coordinates.
What this means, philosophically, can be debated, but it does offer some plausibility to the claim that space and time are auxiliary, conceptual additions to what we actually experience, which just account for the relations between bits of matter. These concepts can be dispensed with even where we have a classical-looking phase space rather than Hilbert space (where, presumably, this is even more true).
…
Edit: On a totally unrelated note, I just noticed this post by Alex Hoffnung over at the n-Category Cafe which gives a lot of detail on issues relating to spans in bicategories that I had begun to think more about recently in relation to developing a higher-gauge-theoretic version of the construction I described for ETQFT. In particular, I’d been thinking about how the 2-group analog of restriction and induction for representations realizes the various kinds of duality properties, where we have adjunctions, biadjunctions, and so forth, in which units and counits of the various adjunctions have further duality. This observation seems to be due to Jim Dolan, as far as I can see from a brief note in HDA II. In that case, it’s really talking about the star-structure of the span (tri)category, but looking at the discussion Alex gives suggests to me that this theme shows up throughout this subject. I’ll have to take a closer look at the draft paper he linked to and see if there’s more to say…
April 6, 2011 at 8:49 am
http://zone-reflex.blogspot.com/2011/03/whats-matrix-relative-locality.html
April 6, 2011 at 1:31 pm
There’s a lot going on there, but what I can think of something to say about is the business about the relationship between “observer” and “consciousness”. I suppose first I should say that “consciousness” in something like the sense it’s used in philosophy of mind (caveat: not a philosopher over here) clearly has a bunch of deep and unresolved issues around it. The meaning of “observer” in quantum mechanics also has various philosophical issues. There’s certainly an old (as old as QM, anyway) and respectable line of thought that they are related or even the same, for reasons to do with the measurement problem, of which Penrose is maybe the best-known recent advocate. Since there are mathematically consistent interpretations (e.g. Everett’s MWI, Rovelli’s relational view) that don’t include wavefunction collapse and assume any entity in the theory is a quantum entity, it’s not so clear to me up front that the two sets of issues have much in common.
In any case, the sense in which Laurent Freidel, at least, takes “observer” in this context is closer to the sense in special relativity. All that the “observer” is assumed to have, is a worldline for a point moving in phase space, and a system of coordinates generated from that, which describes the information the observer can get from the environment (and is, more or less by definition, local around the observer). This came up in a discussion during the break at the workshop – Aleksandr Mikovic was arguing on physical grounds that we do see space phenomenologically because instruments record quantities in space – moving needles on a dial or the like – which has to be seen by an observer who is associated with some extended physical body. Freidel cited his paradigm of an observer as a point-particle like an electron (in this approximation where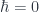 ), which he doesn’t think of as having or needing consciousness. One might avoid part of this argument by taking a concept like Whitehead’s panexperientialist view (caveat again: still not a philosopher over here), and using some word such as “experience” for the sense in which an electron, or anything else, receives information from the parts of its environment it collides with, while reserving “consciousness” for something more like what human beings have.
), which he doesn’t think of as having or needing consciousness. One might avoid part of this argument by taking a concept like Whitehead’s panexperientialist view (caveat again: still not a philosopher over here), and using some word such as “experience” for the sense in which an electron, or anything else, receives information from the parts of its environment it collides with, while reserving “consciousness” for something more like what human beings have.
The remaining debate would be over whether experience in this sense is enough to qualify as an observer, but at least that would be clear. I incline toward “yes” here. It also wouldn’t have much to do, for instance, with Penrose’s thoughts about the need of quantum coherence in the brain, or similiar, which I take to have more to do with philosophy of mind (or perhaps just neuroscience). I don’t know so much about that, but I get the impression neuroscientists think it’s unlikely. Perhaps you have other aspects of this question in mind, I’m not sure.
April 6, 2011 at 5:00 pm
#…and using some word such as “experience” for the sense in which an electron, or anything else, receives information from the parts of its environment it collides with, while reserving “consciousness” for something more like what human beings have.”
Humans have difficulties in abandoning her fancy pictures.
The electron/point/observer is doing a measurement = getting information (as energy in this case on an axis of entropy-negentropy) about the outer world. The process of getting information is basically consciousness.
Human ‘consciousness’ is more like awareness, and because of that we talk of ‘unconsciousness’ for things we are not aware of. But in reality everything is consciousness, and invoke on us and our behavorial output just as much. The awareness can be modified, but not consciousness.
We collect this consciousness in our measurements from outer world, just as the electron does. Living matter has more sophisticated ways to measure negentropy, or the oscillational differencies than electrones and ordinary matter. Also living matter has other ways of treating the energy release from the measurements.
In the light from your post, the least ‘real’ world is our classic world. We can manipulate this ‘realness’ by changing the hbar, and we get maybe the three worlds of Penrose? The psychological one would then be the mind? The geometrical one is particles only, and it will obey the psychological? But underlying must be a common symmetry that will not vanish completely? A ‘conscious’,non-local,’living’ Universe, holding everything together? Maybe without math?
Ulla.
January 11, 2013 at 1:39 pm
Why is the center of mass not considered when thinking of the momentum of macroscopic objects? It seems to me that the momentum space of an object is defined in terms of the objects center of mass, no matter its total mass or components.
January 11, 2013 at 2:26 pm
So, in which context is the centre of mass not being considered?
Of course, you’re right that if we treat a macroscopic object as a single thing (rather than as a large system made of atoms or other smaller parts), then we should be thinking of its centre of mass when we describe its world-line or describe its momentum space. One way this comes up is that authors work in an approximation where the “observer” is small enough that their size/shape as extended objects in space is not relevant, so they’re considered pointlike. Equivalently, we’re only looking at the centre of mass of the observer, who makes observations of momenta of other particles by colliding with them and seeing how that causes the worldline of the observer’s centre of mass to deviate from a geodesic. (Or, if that would be too small to detect, then via a calorimeter, which is indirectly measuring the same thing.)
I guess its’ more likely that you’re referring to the part that addresses the “soccer ball problem”. Maybe the objection comes from these two sentences:
So, again, it’s quite true that we should consider the soccer ball’s centre of mass as its location, and for the purposes of figuring out its momentum. This makes the first sentence seem unnecessarily complicated. But what’s not true is that we should expect the scale at which the curvature of the momentum space to become apparent to be the (momentum equivalent of) the Planck mass scale. That’s what the second sentence is getting at.
The theory as given describes interactions of “fundamental particles”. This is safe to say here because we’re in an approximation where we can ignore strictly quantum-mechanical or quantum-field-theory effects. In this particular limit of whatever the underlying theory may be, we go ahead and think of particles as tiny billiard balls or some such picture. The “soccer ball problem” refers to the fact that a macroscopic object is typically much larger than the Planck mass (about 20 micrograms), so we would naively expect the theory to say that the curvature of momentum space should be immediately visible for such objects.
The point of the second sentence in the quote is that we can indeed use the theory to describe things like soccer balls – and then the momentum space is that of the object’s centre of mass, just like you said. However, that theory has a different mass scale where the curvature of momentum space becomes apparent. (Namely, the scale where the ball’s momentum is such that the individual particles in it have momentum near the original theory’s mass scale.)
The fact that these constants in the theory change with scale shouldn’t be too surprising. Think of viscosity, say: in an approximation where water is a perfect continuous fluid (i.e. we ignore its molecules and just use Navier-Stokes equations or something like that), then changing scale appears to change its behaviour. If we scale up to look at a body of water ten times larger, it will appear to behave as a much less viscous fluid. If we scale down and look at it under a microscope, it will look much more viscous. (Or, to put it another way, you can make a small scale-model of a waterfall, but you need to use something much less viscous than water for it to behave correctly.)
Does that answer make any sense?
January 11, 2013 at 7:08 pm
One more questions. Does the curvature of momentum space have to do with a property of a single object or the relation between properties of a pair of objects?
January 14, 2013 at 11:34 am
I guess the best answer is that it’s about the relation between a pair of objects. It’s the space of observed momenta measured by an observer at any given point. So each measured momentum is a property of the relation between that observer and the object whose momentum is being measured, at the time of measurement.