Higher Gauge Theory in Edinburgh – Part III

Why Higher Geometric Quantization

The largest single presentation was a pair of talks on “The Motivation for Higher Geometric Quantum Field Theory” by Urs Schreiber, running to about two and a half hours, based on these notes. This was probably the clearest introduction I’ve seen so far to the motivation for the program he’s been developing for several years. Broadly, the idea is to develop a higher-categorical analog of geometric quantization (GQ for short).

One guiding idea behind this is that we should really be interested in quantization over (higher) stacks, rather than merely spaces. This leads inexorably to a higher-categorical version of GQ itself. The starting point, though, is that the defining features of stacks capture two crucial principles from physics: the gauge principle, and locality. The gauge principle means that we need to keep track not just of connections, but gauge transformations, which form respectively the objects and morphisms of a groupoid. “Locality” means that these groupoids of configurations of a physical field on spacetime is determined by its local configuration on regions as small as you like (together with information about how to glue together the data on small regions into larger regions).

Some particularly simple cases can be described globally: a scalar field gives the space of all scalar functions, namely maps into ; sigma models generalise this to the space of maps for some other target space. These are determined by their values pointwise, so of course are local.

More generally, physicists think of a field theory as given by a fibre bundle (the previous examples being described by trivial bundles ), where the fields are sections of the bundle. Lagrangian physics is then described by a form on the jet bundle of , i.e. the bundle whose fibre over consists of the space describing the possible first derivatives of a section over that point.

More generally, a field theory gives a procedure for taking some space with structure – say a (pseudo-)Riemannian manifold – and produce a moduli space of fields. The Sigma models happen to be representable functors: for some , the representing object. A prestack is just any functor taking to a moduli space of fields. A stack is one which has a “descent condition”, which amounts to the condition of locality: knowing values on small neighbourhoods and how to glue them together determines values on larger neighborhoods.

The Yoneda lemma says that, for reasonable notions of “space”, the category from which we picked target spaces embeds into the category of stacks over (Riemannian manifolds, for instance) and that the embedding is faithful – so we should just think of this as a generalization of space. However, it’s a generalization we need, because gauge theories determine non-representable stacks. What’s more, the “space” of sections of one of these fibred stacks is also a stack, and this is what plays the role of the moduli space for gauge theory! For higher gauge theories, we will need higher stacks.

All of the above is the classical situation: the next issue is how to quantize such a theory. It involves a generalization of Geometric Quantization (GQ for short). Now a physicist who actually uses GQ will find this perspective weird, but it flows from just the same logic as the usual method.

In ordinary GQ, you have some classical system described by a phase space, a manifold equipped with a pre-symplectic 2-form . Intuitively, describes how the space, locally, can be split into conjugate variables. In the phase space for a particle in -space, these “position” and “momentum” variables, and ; many other systems have analogous conjugate variables. But what really matters is the form itself, or rather its cohomology class.

Then one wants to build a Hilbert space describing the quantum analog of the system, but in fact, you need a little more than to do this. The Hilbert space is a space of sections of some bundle whose sections look like copies of the complex numbers, called the “prequantum line bundle“. It needs to be equipped with a connection, whose curvature is a 2-form in the class of : in general, . (If is not symplectic, i.e. is degenerate, this implies there’s some symmetry on , in which case the line bundle had better be equivariant so that physically equivalent situations correspond to the same state). The easy case is the trivial bundle, so that we get a space of functions, like (for some measure compatible with ). In general, though, this function-space picture only makes sense locally in : this is why the choice of prequantum line bundle is important to the interpretation of the quantized theory.

Since the crucial geometric thing here is a bundle over the moduli space, when the space is a stack, and in the context of higher gauge theory, it’s natural to seek analogous constructions using higher bundles. This would involve, instead of a (pre-)symplectic 2-form , an -form called a (pre-)-plectic form (for an introductory look at this, see Chris Rogers’ paper on the case over manifolds). This will give a higher analog of the Hilbert space.

Now, maps between Hilbert spaces in QG come from Lagrangian correspondences – these might be maps of moduli spaces, but in general they consist of a “space of trajectories” equipped with maps into a space of incoming and outgoing configurations. This is a span of pre-symplectic spaces (equipped with pre-quantum line bundles) that satisfies some nice geometric conditions which make it possible to push a section of said line bundle through the correspondence. Since each prequantum line bundle can be seen as maps out of the configuration space into a classifying space (for , or in general an -group of phases), we get a square. The action functional is a cell that fills this square (see the end of 2.1.3 in Urs’ notes). This is a diagrammatic way to describe the usual GQ construction: the advantage is that it can then be repeated in the more general setting without much change.

This much is about as far as Urs got in his talk, but the notes go further, talking about how to extend this to infinity-stacks, and how the Dold-Kan correspondence tells us nicer descriptions of what we get when linearizing – since quantization puts us into an Abelian category.

I enjoyed these talks, although they were long and Urs came out looking pretty exhausted, because while I’ve seen several others on this program, this was the first time I’ve seen it discussed from the beginning, with a lot of motivation. This was presumably because we had a physically-minded part of the audience, whereas I’ve mostly seen these for mathematicians, and usually they come in somewhere in the middle and being more time-limited miss out some of the details and the motivation. The end result made it quite a natural development. Overall, very helpful!

 

TQFT’s in Vienna – Part 2

To continue from the previous post…

Twisted Differential Cohomology

Ulrich Bunke gave a talk introducing differential cohomology theories, and Thomas Nikolaus gave one about a twisted version of such theories (unfortunately, perhaps in the wrong order). The idea here is that cohomology can give a classification of field theories, and if we don’t want the theories to be purely topological, we would need to refine this. A cohomology theory is a (contravariant) functorial way of assigning to any space , which we take to be a manifold, a -graded group: that is, a tower of groups of “cocycles”, one group for each , with some coboundary maps linking them. (In some cases, the groups are also rings) For example, the group of differential forms, graded by degree.

Cohomology theories satisfy some axioms – for example, the Mayer-Vietoris sequence has to apply whenever you cut a manifold into parts. Differential cohomology relaxes one axiom, the requirement that cohomology be a homotopy invariant of . Given a differential cohomology theory, one can impose equivalence relations on the differential cocycles to get a theory that does satisfy this axiom – so we say the finer theory is a “differential refinement” of the coarser. So, in particular, ordinary cohomology theories are classified by spectra (this is related to the Brown representability theorem), whereas the differential ones are represented by sheaves of spectra – where the constant sheaves represent the cohomology theories which happen to be homotopy invariants.

The “twisting” part of this story can be applied to either an ordinary cohomology theory, or a differential refinement of one (though this needs similarly refined “twisting” data). The idea is that, if is a cohomology theory, it can be “twisted” over by a map into the “Picard group” of . This is the group of invertible -modules (where an -module means a module for the cohomology ring assigned to ) – essentially, tensoring with these modules is what defines the “twisting” of a cohomology element.

An example of all this is twisted differential K-theory. Here the groups are of isomorphism classes of certain vector bundles over , and the twisting is particularly simple (the Picard group in the topological case is just ). The main result is that, while topological twists are classified by appropriate gerbes on (for K-theory, -gerbes), the differential ones are classified by gerbes with connection.

Fusion Categories

Scott Morrison gave a talk about Classifying Fusion Categories, the point of which was just to collect together a bunch of results constructing particular examples. The talk opens with a quote by Rutherford: “All science is either physics or stamp collecting” – that is, either about systematizing data and finding simple principles which explain it, or about collecting lots of data. This talk was unabashed stamp-collecting, on the grounds that we just don’t have a lot of data to systematically understand yet – and for that very reason I won’t try to summarize all the results, but the slides are well worth a look-over. The point is that fusion categories are very useful in constructing TQFT’s, and there are several different constructions that begin “given a fusion category “… and yet there aren’t all that many examples, and very few large ones, known.

Scott also makes the analogy that fusion categories are “noncommutative finite groups” – which is a little confusing, since not all finite groups are commutative anyway – but the idea is that the symmetric fusion categories are exactly the representation categories of finite groups. So general fusion categories are a non-symmetric generalization of such groups. Since classifying finite groups turned out to be difficult, and involve a laundry-list of sporadic groups, it shouldn’t be too surprising that understanding fusion categories (which, for the symmetric case, include the representation categories of all these examples) should be correspondingly tricky. Since, as he points out, we don’t have very many non-symmetric examples beyond rank 12 (analogous to knowing only finite groups with at most 12 elements), it’s likely that we don’t have a very good understanding of these categories in general yet.

There were a couple of talks – one during the workshop by Sonia Natale, and one the previous week by Sebastian Burciu, whom I also had the chance to talk with that week – about “Equivariantization” of fusion categories, and some fairly detailed descriptions of what results. The two of them have a paper on this which gives more details, which I won’t summarize – but I will say a bit about the construction.

An “equivariantization” of a category acted on by a group is supposed to be a generalization of the notion of the set of fixed points for a group acting on a set.  The category has objects which consist of an object which is fixed by the action of , together with an isomorphism for each , satisfying a bunch of unsurprising conditions like being compatible with the group operation. The morphisms are maps in between the objects, which form commuting squares for each . Their paper, and the talks, described how this works when is a fusion category – namely, is also a fusion category, and one can work out its fusion rules (i.e. monoidal structure). In some cases, it’s a “group theoretical” fusion category (it looks like for some group ) – or a weakened version of such a thing (it’s Morita equivalent to ).

A nice special case of this is if the group action happens to be trivial, so that every object of is a fixed point. In this case, is just the category of objects of equipped with a -action, and the intertwining maps between these. For example, if , then (in particular, a “group-theoretical fusion category”). What’s more, this construction is functorial in itself: given a subgroup , we get an adjoint pair of functors between and , which in our special case are just the induced-representation and restricted-representation functors for that subgroup inclusion. That is, we have a Mackey functor here. These generalize, however, to any fusion category , and to nontrivial actions of on . The point of their paper, then, is to give a good characterization of the categories that come out of these constructions.

Quantizing with Higher Categories

The last talk I’d like to describe was by Urs Schreiber, called Linear Homotopy Type Theory for Quantization. Urs has been giving evolving talks on this topic for some time, and it’s quite a big subject (see the long version of the notes above if there’s any doubt). However, I always try to get a handle on these talks, because it seems to be describing the most general framework that fits the general approach I use in my own work. This particular one borrows a lot from the language of logic (the “linear” in the title alludes to linear logic).

Basically, Urs’ motivation is to describe a good mathematical setting in which to construct field theories using ingredients familiar to the physics approach to “field theory”, namely… fields. (See the description of Kevin Walker’s talk.) Also, Lagrangian functionals – that is, the notion of a physical action. Constructing TQFT from modular tensor categories, for instance, is great, but the fields and the action seem to be hiding in this picture. There are many conceptual problems with field theories – like the mathematical meaning of path integrals, for instance. Part of the approach here is to find a good setting in which to locate the moduli spaces of fields (and the spaces in which path integrals are done). Then, one has to come up with a notion of quantization that makes sense in that context.

The first claim is that the category of such spaces should form a differentially cohesive infinity-topos which we’ll call . The “infinity” part means we allow morphisms between field configurations of all orders (2-morphisms, 3-morphisms, etc.). The “topos” part means that all sorts of reasonable constructions can be done – for example, pullbacks. The “differentially cohesive” part captures the sort of structure that ensures we can really treat these as spaces of the suitable kind: “cohesive” means that we have a notion of connected components around (it’s implemented by having a bunch of adjoint functors between spaces and points). The “differential” part is meant to allow for the sort of structures discussed above under “differential cohomology” – really, that we can capture geometric structure, as in gauge theories, and not just topological structure.

In this case, we take to have objects which are spectral-valued infinity-stacks on manifolds. This may be unfamiliar, but the main point is that it’s a kind of generalization of a space. Now, the sort of situation where quantization makes sense is: we have a space (i.e. -object) of field configurations to start, then a space of paths (this is WHERE “path-integrals” are defined), and a space of field configurations in the final system where we observe the result. There are maps from the space of paths to identify starting and ending points. That is, we have a span:

Now, in fact, these may all lie over some manifold, such as , the classifying space for -gerbes. That is, we don’t just have these “spaces”, but these spaces equipped with one of those pieces of cohomological twisting data discussed up above. That enters the quantization like an action (it’s WHAT you integrate in a path integral).

Aside: To continue the parallel, quantization is playing the role of a cohomology theory, and the action is the twist. I really need to come back and complete an old post about motives, because there’s a close analogy here. If quantization is a cohomology theory, it should come by factoring through a universal one. In the world of motives, where “space” now means something like “scheme”, the target of this universal cohomology theory is a mild variation on just the category of spans I just alluded to. Then all others come from some functor out of it.

Then the issue is what quantization looks like on this sort of scenario. The Atiyah-Singer viewpoint on TQFT isn’t completely lost here: quantization should be a functor into some monoidal category. This target needs properties which allow it to capture the basic “quantum” phenomena of superposition (i.e. some additivity property), and interference (some actual linearity over ). The target category Urs talked about was the category of -rings. The point is that these are just algebras that live in the world of spectra, which is where our spaces already lived. The appropriate target will depend on exactly what is.

But what Urs did do was give a characterization of what the target category should be LIKE for a certain construction to work. It’s a “pull-push” construction: see the link way above on Mackey functors – restriction and induction of representations are an example . It’s what he calls a “(2-monoidal, Beck-Chevalley) Linear Homotopy-Type Theory”. Essentially, this is a list of conditions which ensure that, for the two morphisms in the span above, we have a “pull” operation for some and left and right adjoints to it (which need to be related in a nice way – the jargon here is that we must be in a Wirthmuller context), satisfying some nice relations, and that everything is functorial.

The intuition is that if we have some way of getting a “linear gadget” out of one of our configuration spaces of fields (analogous to constructing a space of functions when we do canonical quantization over, let’s say, a symplectic manifold), then we should be able to lift it (the “pull” operation) to the space of paths. Then the “push” part of the operation is where the “path integral” part comes in: many paths might contribute to the value of a function (or functor, or whatever it may be) at the end-point of those paths, because there are many ways to get from A to B, and all of them contribute in a linear way.

So, if this all seems rather abstract, that’s because the point of it is to characterize very generally what has to be available for the ideas that appear in physics notions of path-integral quantization to make sense. Many of the particulars – spectra, -rings, infinity-stacks, and so on – which showed up in the example are in a sense just placeholders for anything with the right formal properties. So at the same time as it moves into seemingly very abstract terrain, this approach is also supposed to get out of the toy-model realm of TQFT, and really address the trouble in rigorously defining what’s meant by some of the standard practice of physics in field theory by analyzing the logical structure of what this practice is really saying. If it turns out to involve some unexpected math – well, given the underlying issues, it would have been more surprising if it didn’t.

It’s not clear to me how far along this road this program gets us, as far as dealing with questions an actual physicist would like to ask (for the most part, if the standard practice works as an algorithm to produce results, physicists seldom need to ask what it means in rigorous math language), but it does seem like an interesting question.

 

HGTQGR – Part IIIb (Workshop)

As usual, this write-up process has been taking a while since life does intrude into blogging for some reason.  In this case, because for a little less than a week, my wife and I have been on our honeymoon, which was delayed by our moving to Lisbon.  We went to the Azores, or rather to São Miguel, the largest of the nine islands.  We had a good time, roughly like so:

Now that we’re back, I’ll attempt to wrap up with the summaries of things discussed at the workshop on Higher Gauge Theory, TQFT, and Quantum Gravity.  In the previous post I described talks which I roughly gathered under TQFT and Higher Gauge Theory, but the latter really ramifies out in a few different ways.  As began to be clear before, higher bundles are classified by higher cohomology of manifolds, and so are gerbes – so in fact these are two slightly different ways of talking about the same thing.  I also remarked, in the summary of Konrad Waldorf’s talk, the idea that the theory of gerbes on a manifold is equivalent to ordinary gauge theory on its loop space – which is one way to make explicit the idea that categorification “raises dimension”, in this case from parallel transport of points to that of 1-dimensional loops.  Next we’ll expand on that theme, and then finally reach the “Quantum Gravity” part, and draw the connection between this and higher gauge theory toward the end.

Gerbes and Cohomology

The very first workshop speaker, in fact, was Paolo Aschieri, who has done a lot of work relating noncommutative geometry and gravity.  In this case, though, he was talking about noncommutative gerbes, and specifically referred to this work with some of the other speakers.  To be clear, this isn’t about gerbes with noncommutative group , but about gerbes on noncommutative spaces.  To begin with, it’s useful to express gerbes in the usual sense in the right language.  In particular, he explain what a gerbe on a manifold is in concrete terms, giving Hitchin’s definition (viz).  A 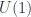gerbe can be described as “a cohomology class” but it’s more concrete to present it as:

• a collection of line bundles associated with double overlaps 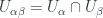.  Note this gets an algebraic structure (multiplication of bundles is pointwise , with an inverse given by the dual, , so we can require…
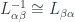• , which helps define…
• transition functions 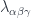on triple overlaps , which are sections of 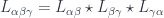.  If this product is trivial, there’d be a 1-cocycle condition here, but we only insist on the 2-cocycle condition…
• 

This is a 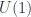-gerbe on a commutative space.  The point is that one can make a similar definition for a noncommutative space.  If the space is associated with the algebra 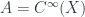of smooth functions, then a line bundle is a module for 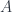, so if 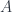is noncommutative (thought of as a “space” ), a “bundle over is just defined to be an 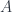-module.  One also has to define an appropriate “covariant derivative” operator 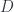on this module, and the -product must be defined as well, and will be noncommutative (we can think of it as a deformation of the above).  The transition functions are sections: that is, elements of the modules in question.  his means we can describe a gerbe in terms of a big stack of modules, with a chosen algebraic structure, together with some elements.  The idea then is that gerbes can give an interpretation of cohomology of noncommutative spaces as well as commutative ones.

Mauro Spera spoke about a point of view of gerbes based on “transgressions”.  The essential point is that an 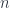-gerbe on a space can be seen as the obstruction to patching together a family of  -gerbes.  Thus, for instance, a 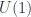0-gerbe is a 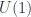-bundle, which is to say a complex line bundle.  As described above, a 1-gerbe can be understood as describing the obstacle to patching together a bunch of line bundles, and the obstacle is the ability to find a cocycle 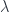satisfying the requisite conditions.  This obstacle is measured by the cohomology of the space.  Saying we want to patch together -gerbes on the fibre.  He went on to discuss how this manifests in terms of obstructions to string structures on manifolds (already discussed at some length in the post on Hisham Sati’s school talk, so I won’t duplicate here).

A talk by Igor Bakovic, “Stacks, Gerbes and Etale Groupoids”, gave a way of looking at gerbes via stacks (see this for instance).  The organizing principle is the classification of bundles by the space maps into a classifying space – or, to get the category of principal -bundles on, the category 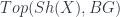, where 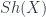is the category of sheaves on and 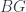is the classifying topos of -sets.  (So we have geometric morphisms between the toposes as the objects.)  Now, to get further into this, we use that 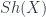is equivalent to the category of Étale spaces over – this is a refinement of the equivalence between bundles and presheaves.  Taking stalks of a presheaf gives a bundle, and taking sections of a bundle gives a presheaf – and these operations are adjoint.

The issue at hand is how to categorify this framework to talk about 2-bundles, and the answer is there’s a 2-adjunction between the 2-category 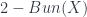of such things, and , the 2-category of fibred categories over .  (That is, instead of looking at “sheaves of sets”, we look at “sheaves of categories” here.)  The adjunction, again, involves talking stalks one way, and taking sections the other way.  One hard part of this is getting a nice definition of “stalk” for stacks (i.e. for the “sheaves of categories”), and a good part of the talk focused on explaining how to get a nice tractable definition which is (fibre-wise) equivalent to the more natural one.

Bakovic did a bunch of this work with Branislav Jurco, who was also there, and spoke about “Nonabelian Bundle 2-Gerbes“.  The paper behind that link has more details, which I’ve yet to entirely absorb, but the essential point appears to be to extend the description of “bundle gerbes” associated to crossed modules up to 2-crossed modules.  Bundles, with a structure-group , are classified by the cohomology with coefficients in ; and whereas “bundle-gerbes” with a structure-crossed-module 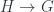can likewise be described by cohomology .  Notice this is a bit different from the description in terms of higher cohomology for a -gerbe, which can be understood as a bundle-gerbe using the shifted crossed module 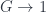(when is abelian.  The goal here is to generalize this part to nonabelian groups, and also pass up to “bundle 2-gerbes” based on a 2-crossed module, or crossed complex of length 2, 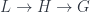as I described previously for Joao Martins’ talk.  This would be classified in terms of cohomology valued in the 2-crossed module.  The point is that one can describe such a thing as a bundle over a fibre product, which (I think – I’m not so clear on this part) deals with the same structure of overlaps as the higher cohomology in the other way of describing things.

Finally,  a talk that’s a little harder to classify than most, but which I’ve put here with things somewhat related to string theory, was Alexander Kahle‘s on “T-Duality and Differential K-Theory”, based on work with Alessandro Valentino.  This uses the idea of the differential refinement of cohomology theories – in this case, K-theory, which is a generalized cohomology theory, which is to say that K-theory satisfies the Eilenberg-Steenrod axioms (with the dimension axiom relaxed, hence “generalized”).  Cohomology theories, including generalized ones, can have differential refinements, which pass from giving topological to geometrical information about a space.  So, while K-theory assigns to a space the Grothendieck ring of the category of vector bundles over it, the differential refinement of K-theory does the same with the category of vector bundles with connection.  This captures both local and global structures, which turns out to be necessary to describe fields in string theory – specifically, Ramond-Ramond fields.  The point of this talk was to describe what happens to these fields under T-duality.  This is a kind of duality in string theory between a theory with large strings and small strings.  The talk describes how this works, where we have a manifold with fibres at each point 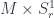with fibres strings of radius and with radius 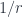.  There’s a correspondence space 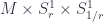, which has projection maps down into the two situations.  Fields, being forms on such a fibration, can be “transferred” through this correspondence space by a “pull-back and push-forward” (with, in the middle, a wedge with a form that mixes the two directions, ).  But to be physically the right kind of field, these “forms” actually need to be representing cohomology classes in the differential refinement of K-theory.

Quantum Gravity etc.

Now, part of the point of this workshop was to try to build, or anyway maintain, some bridges between the kind of work in geometry and topology which I’ve been describing and the world of physics.  There are some particular versions of physical theories where these ideas have come up.  I’ve already touched on string theory along the way (there weren’t many talks about it from a physicist’s point of view), so this will mostly be about a different sort of approach.

Benjamin Bahr gave a talk outlining this approach for our mathematician-heavy audience, with his talk on “Spin Foam Operators” (see also for instance this paper).  The point is that one approach to quantum gravity has a theory whose “kinematics” (the description of the state of a system at a given time) is described by “spin networks” (based on gauge theory), as described back in the pre-school post.  These span a Hilbert space, so the “dynamical” issue of such models is how to get operators between Hilbert spaces from “foams” that interpolate between such networks – that is, what kind of extra data they might need, and how to assign amplitudes to faces and edges etc. to define an operator, which (assuming a “local” theory where distant parts of the foam affect the result independently) will be of the form:

where 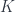is a particular complex (foam), 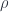is a way of assigning irreps to faces of the foam, and 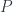is the assignment of intertwiners to edges.  Later on, one can take a discrete version of a path integral by summing over all these 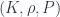.  Here we have a product over faces and one over vertices, with an amplitude 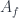assigned (somehow – this is the issue) to faces.  The trace is over all the representation spaces assigned to the edges that are incident to a vertex (this is essentially the only consistent way to assign an amplitude to a vertex).  If we also consider spacetimes with boundary, we need some amplitudes 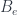at the boundary edges, as well.  A big part of the work with such models is finding such amplitudes that meet some nice conditions.

Some of these conditions are inherently necessary – to ensure the theory is invariant under gauge transformations, or (formally) changing orientations of faces.  Others are considered optional, though to me “functoriality” (that the way of deriving operators respects the gluing-together of foams) seems unavoidable – it imposes that the boundary amplitudes have to be found from the 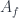in one specific way.  Some other nice conditions might be: that 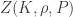depends only on the topology of 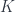(which demands that the 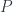operators be projections); that is invariant under subdivision of the foam (which implies the amplitudes have to be ).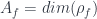

Assuming all these means the only choice is exactly which sub-projection is of the projection onto the gauge-invariant part of the representation space for the faces attached to edge .  The rest of the talk discussed this, including some examples (models for BF-theory, the Barrett-Crane model and the more recent EPRL/FK model), and finished up by discussing issues about getting a nice continuum limit by way of “coarse graining”.

On a related subject, Bianca Dittrich spoke about “Dynamics and Diffeomorphism Symmetry in Discrete Quantum Gravity”, which explained the nature of some of the hard problems with this sort of discrete model of quantum gravity.  She began by asking what sort of models (i.e. which choices of amplitudes) in such discrete models would actually produce a nice continuum theory – since gravity, classically, is described in terms of spacetimes which are continua, and the quantum theory must look like this in some approximation.  The point is to think of these as “coarse-graining” of a very fine (perfect, in the limit) approximation to the continuum by a triangulation with a very short length-scale for the edges.  Coarse graining means discarding some of the edges to get a coarser approximation (perhaps repeatedly).  If the happens to be triangulation-independent, then coarse graining makes no difference to the result, nor does the converse process of refining the triangulation.  So one question is:  if we expect the continuum limit to be diffeomorphism invariant (as is General Relativity), what does this say at the discrete level?  The relation between diffeomorphism invariance and triangulation invariance has been described by Hendryk Pfeiffer, and in the reverse direction by Dittrich et al.

Actually constructing the dynamics for a system like this in a nice way (“canonical dynamics with anomaly-free constraints”) is still a big problem, which Bianca suggested might be approached by this coarse-graining idea.  Now, if a theory is topological (here we get the link to TQFT), such as electromagnetism in 2D, or (linearized) gravity in 3D, coarse graining doesn’t change much.  But otherwise, changing the length scale means changing the action for the continuum limit of the theory.  This is related to renormalization: one starts with a “naive” guess at a theory, then refines it (in this case, by the coarse-graining process), which changes the action for the theory, until arriving at (or approximating to) a fixed point.  Bianca showed an example, which produces a really huge, horrible action full of very complicated terms, which seems rather dissatisfying.  What’s more, she pointed out that, unless the theory is topological, this always produces an action which is non-local – unlike the “naive” discrete theory.  That is, the action can’t be described in terms of a bunch of non-interacting contributions from the field at individual points – instead, it’s some function which couples the field values at distant points (albeit in a way that falls off exponentially as the points get further apart).

In a more specific talk, Aleksandr Mikovic discussed “Finiteness and Semiclassical Limit of EPRL-FK Spin Foam Models”, looking at a particular example of such models which is the (relatively) new-and-improved candidate for quantum gravity mentioned above.  This was a somewhat technical talk, which I didn’t entirely follow, but  roughly, the way he went at this was through the techniques of perturbative QFT.  That is, by looking at the theory in terms of an “effective action”, instead of some path integral over histories 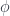with action – which looks like .  Starting with some classical history – a stationary point of the action 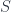– the effective action is an integral over small fluctuations 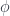around it of .

He commented more on the distinction between the question of triangulation independence (which is crucial for using spin foams to give invariants of manifolds) and the question of whether the theory gives a good quantum theory of gravity – that’s the “semiclassical limit” part.  (In light of the above, this seems to amount to asking if “diffeomorphism invariance” really extends through to the full theory, or is only approximately true, in the limiting case).  Then the “finiteness” part has to do with the question of getting decent asymptotic behaviour for some of those weights mentioned above so as to give a nice effective action (if not necessarily triangulation independence).  So, for instance, in the Ponzano-Regge model (which gives a nice invariant for manifolds), the vertex amplitudes are found by the 6j-symbols of representations.  The asymptotics of the 6j symbols then becomes an issue – Alekandr noted that to get a theory with a nice effective action, those 6j-symbols need to be scaled by a certain factor.  This breaks triangulation independence (hence means we don’t have a good manifold invariant), but gives a physically nicer theory.  In the case of 3D gravity, this is not what we want, but as he said, there isn’t a good a-priori reason to think it can’t give a good theory of 4D gravity.

Now, making a connection between these sorts of models and higher gauge theory, Aristide Baratin spoke about “2-Group Representations for State Sum Models”.  This is a project Baez, Freidel, and Wise, building on work by Crane and Sheppard (see my previous post, where Derek described the geometry of the representation theory for some 2-groups).  The idea is to construct state-sum models where, at the kinematical level, edges are labelled by 2-group representations, faces by intertwiners, and tetrahedra by 2-intertwiners.  (This assumes the foam is a triangulation – there’s a certain amount of back-and-forth in this area between this, and the Poincaré dual picture where we have 4-valent vertices).  He discussed this in a couple of related cases – the Euclidean and Poincaré 2-groups, which are described by crossed modules with base groups or respectively, acting on the abelian group (of automorphisms of the identity) in the obvious way.  Then the analogy of the 6j symbols above, which are assigned to tetrahedra (or dually, vertices in a foam interpolating two kinematical states), are now 10j symbols assigned to 4-simplexes (or dually, vertices in the foam).

One nice thing about this setup is that there’s a good geometric interpretation of the kinematics – irreducible representations of these 2-groups pick out orbits of the action of the relevant 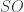on .  These are “mass shells” – radii of spheres in the Euclidean case, or proper length/time values that pick out hyperboloids in the Lorentzian case of .  Assigning these to edges has an obvious geometric meaning (as a proper length of the edge), which thus has a continuous spectrum.  The areas and volumes interpreting the intertwiners and 2-intertwiners start to exhibit more of the discreteness you see in the usual formulation with representations of the 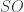groups themselves.  Finally, Aristide pointed out that this model originally arose not from an attempt to make a quantum gravity model, but from looking at Feynman diagrams in flat space (a sort of “quantum flat space” model), which is suggestively interesting, if not really conclusively proving anything.

Finally, Laurent Freidel gave a talk, “Classical Geometry of Spin Network States” which was a way of challenging the idea that these states are exclusively about “quantum geometries”, and tried to give an account of how to interpret them as discrete, but classical.  That is, the quantization of the classical phase space (the cotangent bundle of connections-mod-gauge) involves first a discretization to a spin-network phase space , and then a quantization to get a Hilbert space , and the hard part is the first step.  The point is to see what the classical phase space is, and he describes it as a (symplectic) quotient , which starts by assigning $T^*(SU(2))$ to each edge, then reduced by gauge transformations.  The puzzle is to interpret the states as geometries with some discrete aspect.

The answer is that one thinks of edges as describing (dual) faces, and vertices as describing some polytopes.  For each , there’s a -dimensional “shape space” of convex polytopes with -faces and a given fixed area 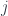.  This has a canonical symplectic structure, where lengths and interior angles at an edge are the canonically conjugate variables.  Then the whole phase space describes ways of building geometries by gluing these things (associated to vertices) together at the corresponding faces whenever the two vertices are joined by an edge.  Notice this is a bit strange, since there’s no particular reason the faces being glued will have the same shape: just the same area.  An area-1 pentagon and an area-1 square associated to the same edge could be glued just fine.  Then the classical geometry for one of these configurations is build of a bunch of flat polyhedra (i.e. with a flat metric and connection on them).  Measuring distance across a face in this geometry is a little strange.  Given two points inside adjacent cells, you measure orthogonal distance to the matched faces, and add in the distance between the points you arrive at (orthogonally) – assuming you glued the faces at the centre.  This is a rather ugly-seeming geometry, but it’s symplectically isomorphic to the phase space of spin network states – so it’s these classical geometries that spin-foam QG is a quantization of.  Maybe the ugliness should count against this model of quantum gravity – or maybe my aesthetic sense just needs work.

(Laurent also gave another talk, which was originally scheduled as one of the school talks, but ended up being a very interesting exposition of the principle of “Relativity of Localization”, which is hard to shoehorn into the themes I’ve used here, and was anyway interesting enough that I’ll devote a separate post to it.)

 

Starting out at IST; Quantales

As I mentioned in my previous post, I’ve recently started out a new postdoc at IST – the Instituto Superior Tecnico in Lisbon, Portugal.  Making the move from North America to Europe with my family was a lot of work – both before and after the move – involving lots of paperwork and shifting of heavy objects.  But Lisbon is a good city, with lots of interesting things to do, and the maths department at IST is very large, with about a hundred faculty.  Among those are quite a few people doing things that interest me.

The group that I am actually part of is coordinated by Roger Picken, and has a focus on things related to Topological Quantum Field Theory.  There are a couple of postdocs and some graduate students here associated in some degree with the group, and elsewhere than IST Aleksandar Mikovic and Joao Faria Martins.   In the coming months there should be some activity going on in this group which I will get to talk about here, including a workshop which is still in development, so I’ll hold off on that until there’s an official announcement.

Quantales

I’ve also had a chance to talk a bit with Pedro Resende, mostly on the subject of quantales.  This is something that I got interested in while at UWO, where there is a large contingent of people interested in category theory (mostly from the point of view of homotopy theory) as well as a good group in noncommutative geometry.  Quantales were originally introduced by Chris Mulvey – I’ve been looking recently at a few papers in which he gives a nice account of the subject – here, here, and here.
The idea emerged, in part, as a way of combining two different approaches to generalising the idea of a space.  One is the approach from topos theory, and more specifically, the generalisation of topological spaces to locales.  This direction also has connections to logic – a topos is a good setting for intuitionistic, but nevertheless classical, logic, whereas quantales give an approach to quantum logics in a similar spirit.

The other direction in which they generalize space is the -algebra approach used in noncommutative geometry.  One motivation of quantales is to say that they simultaneously incorporate the generalizations made in both of these directions – so that both locales and -algebras will give examples.  In particular, a quantale is a kind of lattice, intended to have the same sort of relation to a noncommutative space as a locale has to an ordinary topological space.  So to begin, I’ll look at locales.

A locale is a lattice which formally resembles the lattice of open sets for such a space.  A lattice is a partial order with operations (“meet”) and (“join”).  These operations take the role of the intersection and union of open sets.  So to say it formally resembles a lattice of open sets means that the lattice is closed under arbitrary joins, and finite meets, and satisfies the distributive law:

Lattices like this can be called either “Frames” or “Locales” – the only difference between these two categories is the direction of the arrows.  A map of lattices is a function that preserves all the structure – order, meet, and join.   This is a frame morphism, but it’s also a morphism of locales in the opposite direction.  That is, .

Another name for this sort of object is a “Heyting algebra”.  One of the great things about topos theory (of which this is a tiny starting point) is that it unifies topology and logic.  So, the “internal logic” of a topos has a Heyting algebra (i.e. a locale) of truth values, where the meet and join take the place of logical operators “and” and “or”.  The usual two-valued logic is the initial object in , so while it is special, it isn’t unique.  One vital fact here is that any topological space (via the lattice of open sets) produces a locale, and the locale is enough to identify the space – so is an embedding.  (For convenience, I’m eliding over the fact that the spaces have to be “sober” – for example, Hausdorff.)  In terms of logic, we could imagine that the space is a “state space”, and the truth values in the logic identify for which states a given proposition is true.  There’s nothing particularly exotic about this: “it is raining” is a statement whose truth is local, in that it depends on where and when you happen to look.

To see locales as a generalisation of spaces, it helps to note that the embedding above is full – if and are locales that come from topological spaces, there are no extra morphisms in that don’t come from continuous maps in .  So the category of locales makes the category of topological spaces bigger only by adding more objects – not inventing new morphisms.  The analogous noncommutative statement turns out not to be true for quantales, which is a little red-flag warning which Pedro Resende pointed out to me.

What would this statement be?  Well, the noncommutative analogue of the idea of a topological space comes from another embedding of categories.  To start with, there is an equivalence : the category of locally compact, Hausdorff, topological spaces is (up to equivalence) the opposite of the category of commutative -algebras.  So one simply takes the larger category of all -algebras (or rather, its opposite) as the category of “noncommutative spaces”, which includes the commutative ones – the original locally compact Hausdorff spaces.  The correspondence between an algebra and a space is given by taking the algebra of functions on the space.

So what is a quantale?  It’s a lattice which is formally similar to the lattice of subspaces in some -algebra.  Special elements – “right”, “left,” or “two-sided” elements – then resemble those subspaces that happen to be ideals.  Some intuition comes from thinking about where the two generalizations coincide – a (locally compact) topological space.  There is a lattice of open sets, of course.  In the algebra of continuous functions, each open set determines an ideal – namely, the subspace of functions which vanish on .  When such an ideal is norm-closed, it will correspond to an open set (it’s easy to see that continuous functions which can be approximated by those vanishing on an open set will also do so – if the set is not open, this isn’t the case).

So the definition of a quantale looks much like that for a locale, except that the meet operation is replaced by an associative product, usually called .  Note that unlike the meet, this isn’t assumed to be commutative – this is the point where the generalization happens.  So in particular, any locate gives a quantale with .  So does any -algebra, in the form of its lattice of ideals.  But there are others which don’t show up in either of these two ways, so one might hope to say this is a nice all-encompassing generalisation of the idea of space.

Now, as I said, there was a bit of a warning that comes attached to this hope.  This is that, although there is an embedding of the category of -algebras into the category of quantales, it isn’t full.  That is, not only does one get new objects, one gets new morphisms between old objects.  So, given algebras and , which we think of as noncommutative spaces, and a map of algebras between them, we get a morphism between the associated quantales – lattice maps that preserve the operations.  However, unlike what happened with locales, there are quantale morphisms that don’t correspond to algebra maps.  Even worse, this is still true even in the case where the algebras are commutative, and just come from locally compact Hausdorff spaces: the associated quantales still may have extra morphisms that don’t come from continuous functions.

There seem to be three possible attitudes to this situation.  First, maybe this is just the wrong approach to generalising spaces altogether, and the hints in its favour are simply misleading.  Second, maybe quantales are absolutely the right generalisation of space, and these new morphisms are telling us something profound and interesting.  The third attitude, which Pedro mentioned when pointing out this problem to me, seems most likely, and goes as follows.  There is something special that happens with -algebras, where the analytic structure of the norm makes the algebras more rigid than one might expect.  In algebraic geometry, one can take a space (algebraic variety or scheme) and consider its algebra of global functions.  To make sure that an algebra map corresponds to a map of schemes, though, one really needs to make sure that it actually respects the whole structure sheaf for the space – which describe local functions.  When passing from a topological space to a -algebra, there is a norm structure that comes into play, which is rigid enough that all algebra morphisms will automatically do this – as I said above, the structure of ideals of the algebra tells you all about the open sets.  So the third option is to say that a quantale in itself doesn’t quite have enough information, and one needs some extra data something like the structure sheaf for a scheme.  This would then pick out which are the “good” morphisms between two quantales – namely, the ones that preserve this extra data.  What, precisely, this data ought to be isn’t so clear, though, at least to me.

So there are some complications to treating a quantale as a space.  One further point, which may or may not go anywhere, is that this type of lattice doesn’t quite get along with quantum logic in quite the same way that locales get along with (intuitionistic) classical logic (though it does have connections to linear logic).

In particular, a quantale is a distributive lattice (though taking the product, rather than , as the thing which distributes over ), whereas the “propositional lattice” in quantum logic need not be distributive.  One can understand the failure of distributivity in terms of the uncertainty principle.  Take a statement such as “particle has momentum and is either on the left or right of this barrier”.  Since position and momentum are conjugate variables, and momentum has been determined completely, the position is completely uncertain, so we can’t truthfully say either “particle has momentum and is on the left or “particle has momentum and is on the right”.  Thus, the combined statement that either one or the other isn’t true, even though that’s exactly what the distributive law says: “P and (Q or S) = (P and Q) or (P and S)”.

The lack of distributivity shows up in a standard example of a quantum logic.  This is one where the (truth values of) propositions denote subspaces of a vector space .  “And” (the meet operation ) denotes the intersection of subspaces, while “or” (the join operation ) is the direct sum .  Consider two distinct lines through the origin of – any other line in the plane they span has trivial intersection with either one, but lies entirely in the direct sum.  So the lattice of subspaces is non-distributive.  What the lattice for a quantum logic should be is orthocomplemented, which happens when has an inner product – so for any subspace , there is an orthogonal complement .

Quantum logics are not very good from a logician’s point of view, though – lacking distributivity, they also lack a sensible notion of implication, and hence there’s no good idea of a proof system.  Non-distributive lattices are fine (I just gave an example), and very much in keeping with the quantum-theoretic strategy of replacing configuration spaces with Hilbert spaces, and subsets with subspaces… but viewing them as logics is troublesome, so maybe that’s the source of the problem.

Now, in a quantale, there may be a “meet” operation, separate from the product, which is non-distributive, but if the product is taken to be the analog of “and”, then the corresponding logic is something different.  In fact, the natural form of logic related to quantales is linear logic. This is also considered relevant to quantum mechanics and quantum computation, and as a logic is much more tractable.  The internal semantics of certain monoidal categories – namely, star-autonomous ones (which have a nice notion of dual) – can be described in terms of linear logic (a fairly extensive explanation is found in this paper by Paul-André Melliès).

Part of the point in the connection seems to be resource-limitedness: in linear logic, one can only use a “resource” (which, in standard logic, might be a truth value, but in computation could be the state of some memory register) a limited number of times – often just once.  This seems to be related to the noncommutativity of in a quantale.  The way Pedro Resende described this to me is in terms of observations of a system.  In the ordinary (commutative) logic of a locale, you can form statements such as “A is true, AND B is true, AND C is true” – whose truth value is locally defined.  In a quantale, the product operation allows you to say something like “I observed A, AND THEN observed B, AND THEN observed C”.  Even leaving aside quantum physics, it’s not hard to imagine that in a system which you observe by interacting with it, statements like this will be order-dependent.  I still don’t quite see exactly how these two frameworks are related, though.

On the other hand, the kind of orthocomplemented lattice that is formed by the subspaces of a Hilbert space CAN be recovered in (at least some) quantale settings.  Pedro gave me a nice example: take a Hilbert space , and the collection of all projection operators on it, .  This is one of those orthocomplemented lattices again, since projections and subspaces are closely related.  There’s a quantale that can be formed out of its endomorphisms, , where the product is composition.  In any quantale, one can talk about the “right” elements (and the “left” elements, and “two sided” elements), by analogy with right/left/two-sided ideals – these are elements which, if you take the product with the maximal element, , the result is less than or equal to what you started with: means is a right element.  The right elements of the quantale I just mentioned happen to form a lattice which is just isomorphic to .

So in this case, the quantale, with its connections to linear logic, also has a sublattice which can be described in terms of quantum logic.  This is a more complicated situation than the relation between locales and intuitionistic logic, but maybe this is the best sort of connection one can expect here.

In short, both in terms of logic and spaces, hoping quantales will be “just” a noncommutative variation on locales seems to set one up to be disappointed as things turn out to be more complex.  On the other hand, this complexity may be revealing something interesting.

Coming soon: summaries of some talks I’ve attended here recently, including Ivan Smith on 3-manifolds, symplectic geometry, and Floer cohomology.

 

Recent Talk: Emre Coskun on Gerbes and Stacks

I recently went to California to visit Derek Wise at UC Davis – we were talking about expanding the talk he gave at Perimeter Institute into a more developed paper about ETQFT from Lie groups. Between that, the end of the Winter semester, and the beginning of the “Summer” session (in which I’m teaching linear algebra), it’s taken me a while to write up Emre Coskun’s two-part talk in our Stacks And Groupoids seminar.

Emre was explaining the theory of gerbes in terms of stacks. One way that I have often heard gerbes explained is in terms of a categorification of vector bundles – thus, the theory of “bundle gerbes”, as described by Murray in this paper here. The essential point of that point of view is that bundles can be put together by taking trivial bundles on little neighbourhoods of a space, and “gluing” them together on two-fold overlaps of those neighbourhoods – the gluing functions then have to satisfy a cocycle condition so that they agree on triple overlaps. A gerbe, on the other hand, defines line bundles (not functions) on double overlaps, and the gluing functions now live on triple overlaps. The idea is that this begins a heirarchy of concepts, each of which categorifes the previous (after “gerbe”, one just starts using terms like “2-gerbe”, “3-gerbe”, and so on). The levels of this hierarchy are supposed to be related to the various (nonabelian) cohomology groups of a space . I’ve mostly seen this point of view related to work by Jean-Luc Brylinski. It is a very differential-geometric sort of construction.

Emre, on the other hand, was describing another side to the theory of gerbes, which comes out of algebraic geometry, and is closely related to stacks. There’s a nice survey by Moerdijk which gives an account of gerbes from a similar point of view, though for later material, Emre said he drew on this book by Laumon and Moret-Bailly (which I can only find in the original French). As one might expect, a stack-theoretic view of gerbes thinks of them as generalizations of sheaves, rather than bundles. (The fact that there is a sheaf of sections of a bundle also generalizes to gerbes, so bundle-gerbes are a special case of this point of view).

Gerbes

So the setup is that we have some space – Emre was talking about the context of algebraic geometry, so the relevant idea of space here is scheme (which, if you’re interested, is assumed to have the etale topology – i.e. the one where covers use etale maps, the analog of local isomorphisms).  In the second talk, he generalized this to -spaces: for some chosen scheme .  That is, the category of “spaces” is based on the slice category of schemes equipped with maps into , with the obvious morphisms.  This is a site, since there’s a notion of a cover over and so forth; an -space is a sheaf (of sets) on this site.  So in particular, a scheme over determines an -space, where by .  (That is, the usual way a space determines a representable sheaf).  There are also differential-geometric versions of gerbes.

So, whatever the right notion of space, a stack over a space (in the sense of a sheaf of groupoids over , which we’re assuming has the etale topology) is a gerbe if a couple of nice conditions apply:

1. There’s a cover , such that none of the is empty.
2. Over any open , all the objects are isomorphic (i.e. is connected as a category)

Notice that there doesn’t have to be a global object – that is, needn’t be empty – only some cover such that local objects exist – but where they do, they’re all “the same”.  These conditions can also be summarized in terms of the fibred category .  There are two maps from – the projection and the diagonal.  The conditions respectively say these two maps are, locally, epi (i.e. surjective).

Emre’s first talk began by giving some examples of gerbes to motivate the rest. The first one is the “gerbe of splittings” of an Azumaya algebra. “An” Azumaya algebra is actually a sheaf of algebras over some scheme . The defining property is that locally it looks like the algebra of endomorphisms of a vector bundle. That is, on any neighborhood , we have:

for some (algebraic) vector bundle . A special case is when is just a point, in which case an Azumaya algebra is the same thing as a matrix algebra . So Azumaya algebras are not too complicated to describe.

The gerbe of splittings, for an Azumaya algebra is also not too complicated: a splitting is a way to represent an algebra as endomorphisms of a vector bundle – which in this case may only be possible locally. Over an given , its objects are pairs , where is a vector bundle over , and is an isomorphism. The morphisms are bundle isomorphisms that commute with the . So, roughly: if is locally isomorphic to endomorphisms of vector bundles, the gerbe of splittings is the stack of all the vector bundles and isomorphisms which make this work. It’s easy to see this is a gerbe, since by definition, such bundles must exist locally, and necessarily they’re all isomorphic.

(This example – a gerbe consisting, locally, of a category of all vector bundles of a certain form – starts to suggest why one might want to think of gerbes as categorifying bundles.)

Another easily constructed gerbe in a similar spirit is found from a complex line bundle over (and ). Then is a gerbe over , where the groupoid over a neighborhood has, as objects, pairs where is an isomorphism of line bundles. That is, the objects locally look like roots of . The gerbe is trivial (has a global object) if has a root.

Cohomology

One says that a gerbe is banded by a sheaf of groups on (or is the band of the gerbe, or is a -gerbe), if there are isomorphisms between the group and the automorphism group for each object over (the property of a gerbe means these are all isomorphic). (These isomorphisms should also commute with the group homomorphisms induced by maps of open sets.) So the band is, so to speak, the “local symmetry group over ” of the gerbe in a natural way.

In the case of the gerbe of splittings of above, the band is , where over any given neighborhood, , where is the group of units in the base field: that is, the group consists of all the invertible sections in the structure sheaf of . These get turned into bundle-automorphisms by taking a function to the automorphism that acts through multiplication by . The gerbe associated to a line bundle is banded by the group of -roots of unity in sections in the structure sheaf.

From here, we can see how gerbes relate to cohomology. In particular, a -gerbe , we can associate a cohomology class . This class can be thought of as “the obstruction to the existence of a global object”. So, in the case of an Azumaya algebra, it’s the obstruction to being split (i.e. globally).

The way this works is, given a covering with an object in , we take pull back this object along the morphisms corresponding to inclusions of sub-neighbourhoods, down to a triple-overlap . Then there are isomorphisms comparing the different pullbacks: , and so on. (The lowered indices denote which of the we’re pulling back from).

Then we get a 2-cocycle in (an isomorphism corresponding to what, for sheaves of sets, would be an identity). This is . The existence of this cocycle means that we’re getting an element in , which we denote . If a global object exists, then all our local objects are restrictions of a global one, the cocycle will always turn out to be the identity, so this class is trivial. A non-trivial class implies an obstruction to gluing the local objects into global ones.

Moduli Spaces

In the second talk, Emre gave some more examples of gerbes which it makes sense to think of as moduli spaces, including one which any gerbe resembles locally.

The first is the moduli space of all vector bundles over some (smooth, projective) curve .  (Actually, one looks at those of some particular degree and rank , and requires a condition called stability).

Actually, as discussed earlier in the seminar back in Aji’s talk, the right way to see this is that there is a “fine” moduli space – really a stack and not necessarily a space (in whichever context) – called , and also a “coarse” moduli space called .  Roughly, the actual space has points which are the isomorphism classes of vector bundles, while the stack remembers the whole groupoid of bundles and bundle-isomorphisms.  So there’s a map, which squashes a bundle to its isomorphism class: making the fine moduli space into a category fibred in groupoids – more than that, it’s a stack – and more than that, it’s a gerbe.  That is, there’s always a cover of such that there are some bundles locally, and (stable) bundles of a given rank and degree are always isomorphic.  In fact, this is a -gerbe, as above.

The next example is the gerbe of -torsors, for a group (that is, -sets which are isomorphic as -sets to – the intuition is that they’re just like the group, but without a specified identity). The category consists of -torsors and their isomorphisms.  This is a gerbe over the point .  More interesting, when we’re in the context of -spaces (and has a trivial action of on it), it becomes a -gerbe over .  Part of the point here is that any trivial gerbe (i.e. one with a section) is just such a classifying space for some group.  In particular, for the group of isomorphisms from a particular object to itself, crossed with .

Since any gerbe has sections locally (that is, objects in for some ), every gerbe locally looks like one of these classifying-space gerbes.  This is the analog to the fact that any bundle locally looks like a product.

 

Recent Talks on Stacks and Descent

Among the talks given in our seminar on stacks and groupoids, there have been a few which I haven’t posted about yet – two by Tom Prince about stacks and homotopy theory, and one by José Malagon-Lopez comparing different characterizations of stacks. Tom is a grad student, and José is a postdoc, and they both work with Rick Jardine, who has done a lot of important work in homotopy theory, notably from the simplicial point of view. There was some overlap, since José was comparing the different characterizations for stacks that had been used by different people through the seminar, including Tom, but there’s still quite a lot to say here. I’ll try to cover the main points as I understand them, focusing on what I personally find relevant.

A major theme for both of them is the use of descent, which in general is a way to talk about the objects of a category in terms of another category. A standard example of descent would be the case of sheaves. First, though, what is it that’s being described in terms of descent?

Well, there are two opposite points of view on stacks – as categories fibred in groupoids (CFG’s), and as sheaves of groupoids. (I’ve found this book by Behrend et al. on algebraic stacks handy in parsing through some of the definitions here, and Jose recommended Vistoli’s notes on sites, fibred categories, and descent) One of the things Jose summarized in his talk was how these are related (which was a key bit of Aji’s earlier talk, blogged here). A CFG over is a functor where the preimage over is a groupoid (that is, all the morphisms mapping to an identity are invertible).

Now, given such one gets a (weak) functor from into groupoids (the “fibre-selecting” functor, which, among other conditions, gives the groupoid for each object . Specifying this and showing it is a weak functor takes a little work. But in particular, there are properties on CFG’s a stack is such a functor into with the extra property that descent data are effective. This is a weak version of the condition for a sheaf.

Stacks and Descent

The classical setting for descent questions is sheaf theory. To begin with, we have some category of spaces – this might be (topological spaces), or (affine schemes), or something else – the classical version has , the category of open sets on a topological space. The main thing is that must be a Grothendieck site; in particular, there is a notion of covering for an object . This is a collection of arrows satisfying some conditions that capture the intuitive idea of “open cover”.

So, just to recall: the idea of describing a space as a sheaf on a site involves a little shift of perspective, but it’s the idea behind diffeological spaces (as I described in my post on Enxin Wu’s talk in our seminar, and which, for me, is a good example to help understand this viewpoint). A diffeological space is determined by giving the set of all “smooth” maps into it from each object in a certain site. Now, any space can also be represented in (by the Yoneda embedding) as the sheaf which gives, for each space , the set of maps in (topological, algebraic, or whatever) into – but one can get objects in a bigger category, namely that of sheaves, which is a way of describing them in terms of the objects in the site . In the case of diffeological spaces, the site in question is just the one consisting of neighborhoods in for any , with smooth maps, and the obvious idea of a cover. So representable ones are just Euclidean neighborhoods, and general ones are defined by smooth maps out of these: the sheaf condition is just a way to state the natural compatibility condition for these maps. Similar thinking applies to any site .

The point of this condition is to ask when we can take a cover of an object , and describe global objects (functions on ) in terms of local objects (functions on elements in the cover), which are compatible. Descent is the gluing condition for a sheaf : given a cover – a bunch of maps which satisfy some conditions that capture the intuitive idea of covering – a descent datum is a collection of , and isomorphisms between the restrictions (by ) to overlaps , where the isomorphisms satisfy some cocycle condition ensuring that restrictions to are equal. The datum is effective if all there is a “global” object where is the restriction of . (I find this easiest to see when , where it says we can glue functions on local patches that agree on overlaps, and find that they must have come by restricting a global function on .)

This all makes sense if has values in (or some other 1-category), but the point for stacks is that we have a weak functor . That is, the values are in groupoids, which naturally form a 2-category. So the descent can be weakened – instead of an equality in the cocycle condition, we get an isomorphism, which has to be coherent. Part of the point of describing stacks as “sheaves of groupoids” is as a weakening this way of describing a space, to an “up to equivalence” kind of condition.

One point which Jose made, and which Tom made use of, is that this description of a Grothendieck topology really gives too much information – that is, the category of sheaves on a site (taken up to equivalence) doesn’t uniquely determine the site. Instead of coverings, one should talk about sieves – these are, one might say, one-sided ideals of maps into . In particular, subfunctors – that is, for each space , a subset of all maps , in a way that gets along with composition of maps (which is how they resemble ideals). Any covering defines a seive – as the subfunctor of maps which factor through the covering maps – but more than one covering might define the same sieve (rather the same way an ideal can be presented in terms of different generators).

So the view of stacks as sheaves (of groupoids) satisfying descent is then rephrased by saying that, for any covering sieve of an object , there is an equivalence of functors between and , where and are some sheaves on constructed in a fairly natural way from the object itself, and from the sieve . The point is that is a groupoid. The functor ends up such that can be described in terms of covers as having objects which are compatible collections of objects from and isomorphisms between their restrictions – that is, descent data – and morphisms being compatible maps. So equivalence of these (2-)functors ends up being the stack condition.

One of Tom’s objectives was to look at all this from the point of view of simplicial sheaves – and here we need to think about homotopy-theoretic ideas of “equivalence”, instead of just the equivalence of categories we just used.

Model Structure

One of the major tools in homotopical algebra is the notion of a model structure (these slides by Peter May give the basic concepts). These show up throughout higher category theory because homotopies-between-homotopies-…-between-maps give a natural model of higher morphisms.

Model categories axiomatize three special kinds of maps one is interested in when talking about maps between spaces, up to homotopy. “Weak equivalence” generalizes a “homotopy equivalence” – a map which induces isomorphisms between homotopy groups of and (as far as homotopy theory can detect, and are “the same”). “Fibration” and “cofibration” are defined in homotopy theory by a lifting property (and its dual) – essentially, that if a map can be lifted along , so can a homotopy of the map.  Fibrations generalize (“nice”) surjections, and cofibrations generalize (“nice”) inclusions.

In particular, Tom was making use of a notion of descent where the equations that define the descent conditions are just required to be weak equivalences. The point is that we can talk about sheaves of various kinds of things – sets, groupoids, or simplicial sets were the examples he gave. The relevant notion of equivalence for sets is isomorphism (the usual way of stating descent), but for groupoids it’s equivalence, and for simplicial sets, it’s another notion of weak equivalence (from the Joyal-Tierney model structure). When talking about stacks, we’re dealing with groupoids.

On the other hand, groupoids can be described in terms of simplicial sets, using the construction known as the simplicial nerve. In particular the classifying spaces of groupoids have no interesting homotopy groups above the first – so this ends up giving another way to state the weakened form of descent mentioned above. This type of construction – using the fact that simplicial sets are very versatile (can describe categories, or reasonable spaces, one -categories, for instance), is what makes the study of simplicial presheaves, which is the basis of a lot of work by Rick Jardine (see the book Simplicial Homotopy Theory for a whole lot more that I can touch on here).

This gives another characterization of stacks: a sheaf of groupoids is a stack if and only if (sheaf of classfying spaces), satisfies descent in that it is “pointwise” (that is, section-wise) weakly-equivalent to a certain kind of “globally fibrant replacement”. This is like the description of descent in terms of an equivalence of categories, as above – but in general is weaker. In fact, when the simplicial sets we’re talking about are classifying spaces for groupoids, then by construction these are just the same. This kind of replacement accomplishes for stacks roughly what “sheafification” does for sheaves – i.e. turns “prestacks” into “stacks”. This is done by taking a limit over all sieves – the universal property of the limit, then, is what ensures the existence of all the global objects that descent requires must exist. This is always a “local” weak equivalence, but only if we started with a stack is it one “pointwise” (i.e. in terms of sections).

Cocycles

As an aside: one thing which Tom talked about as a preliminary, but which I found particularly helpful from where I was coming from, had to do with “cocycle categories”. This is a somewhat unusual use of the term “cocycle”: here, a cocycle from to is a certain kind of span – namely, a pair of maps from :

where is a “weak equivalence”. A morphism between cocycles is just a map which commutes with those in the cocycle. These form a category . The point of introducing this is to say that there is a correspondence between components in this category – that is, and homotopy classes of maps from to (the collection of which is denoted in homotopy theory).

One way to think about this is that cocycles stand in relation to functions, roughly, as spans stand to relations. If we are in , where weak equivalence is isomorphism, then can be thought of as the graph of a function from to – since is bijective, can stand as a substitute for . Moving to spaces, we weaken the requirement so that is only a replacement for “up to homotopy” – thus, cocycles are adequate replacements for homotopy classes of functions. This business of replacing objects with other, nicer objects (say, “fibrant replacement”) is a recurring theme in homotopy theory. This digression on cocycles helped me understand why. Part of the point is that the equivalence classes of these “cocycles” is easier to calculate directly than, but equivalent to, homotopy classes of maps.

---

In any case, there’s more I could say about these talks, but I’ll leave off for now.

Over the next week, I’ll be visiting Derek Wise at UC Davis, to talk about some stuff having to do with ETQFT’s , but soon enough I’ll also do a writeup of Emre Coskun’s talks in the seminar about gerbes, which started today and continue tomorrow.